并查集

一、什么是并查集

一种很不一样的树形结构

连接问题——Connectivity Problem

问题抛出

如果我们想知道左上角的这个点和右下角的点有没有连接问题，我们应该怎么做到呢，我们现在就只会用肉眼来看，但是我们将要学习的并查集就可以用来解决这种问题！

• 网络中节点间的链接状态
  • 网络是个抽象的概念：用户之间形成的网络
  • 数学中的集合类实现

连接问题和路径问题

连接问题比路径问题要回答的问题少

温馨提示

如果我们回答路径问题，那么我们会消耗一些不必要的性能，因为有些时候我们只需要知道他们两个之间有没有连接，我们并不需要知道他的路径，也不想知道他们两个是怎么连接的，所以我们如果求他的路径，会有不必要的消耗

public interface UF {
    int getSize();

    boolean isConnected(int p, int q);

    void unionElements(int p, int q);

}

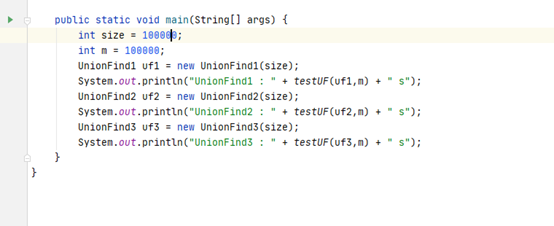
二、Quick Find

package UnionFind;

/**
 * 数组并查集
 */
public class UnionFind1 implements UF {
    private int[] id;
    public UnionFind1(int size){
        id = new int[size];
        for (int i=0;i<id.length;i++){
            id[i] = i;
        }
    }
    @Override
    public int getSize() {
        return id.length;
    }

    // 查找元素p所对应的集合编号
    private int find(int p){
        if (p<0 && p>=id.length){
            throw new IllegalArgumentException("p is out of bound.");
        }
        return id[p];
    }

    // 查看元素p和元素q是否所属一个集合
    @Override
    public boolean isConnected(int p, int q) {
        return find(p) == find(q);
    }

    @Override
    public void unionElements(int p, int q) {
        int pID = find(p);
        int qID = find(q);
        if (pID==qID){
            return;
        }
        for (int i=0;i<id.length;i++){
            if (id[i] == pID){
                id[i] = qID;
            }
        }
    }
}

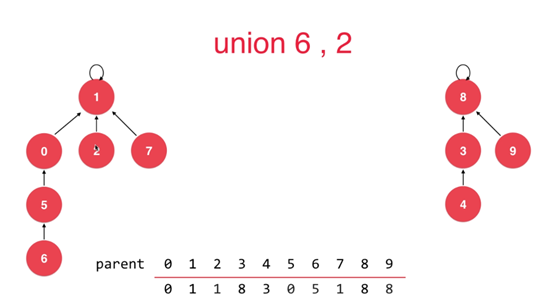
三、Quick Union

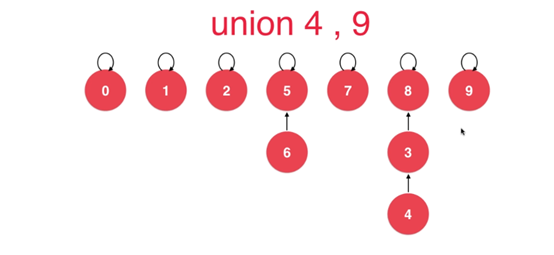
将每一个元素，看做是一个节点

package UnionFind;

/**
 * 第一版树的并查集
 */
public class UnionFind2 implements UF {
    private int[] parent;

    public UnionFind2(int size) {
        parent = new int[size];
        for (int i = 0; i < size; i++) {
            parent[i] = i;
        }
    }

    @Override
    public int getSize() {
        return parent.length;
    }

    // 查找过程，查找元素p所对应的集合编号
    // O（h）复杂度，h为树的高度
    private int find(int p) {
        while (p != parent[p]) {
            p = parent[p];
        }
        return p;
    }

    // 查看元素p和元素q是否所属一个集合
    // O(h)复杂度，h为树的高度
    @Override
    public boolean isConnected(int p, int q) {

        return find(p) == find(q);
    }

    // 合并元素p和元素q所属的集合
    // O（h）复杂度，h为树的高度
    @Override
    public void unionElements(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        if (pRoot == qRoot) {
            return;
        }
        parent[pRoot] = qRoot;
    }
}

我们这里可以看出来我们用数组和用树（其实应该说是森林）之间的区别

温馨提示

如果我们要判断6和4的是不是连接着的，那么我们需要看他们两个相对应的根节点，我们可以看到6的根节点是1，而4的根节点是8，由此可见，他们两个并不是相连接的。

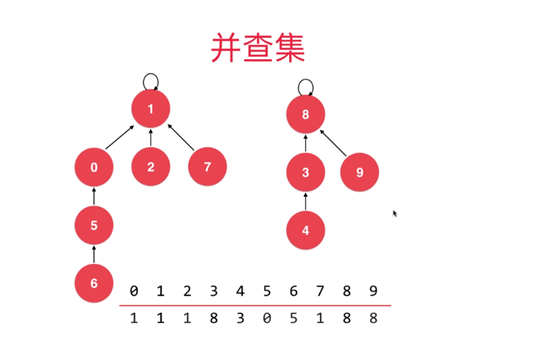
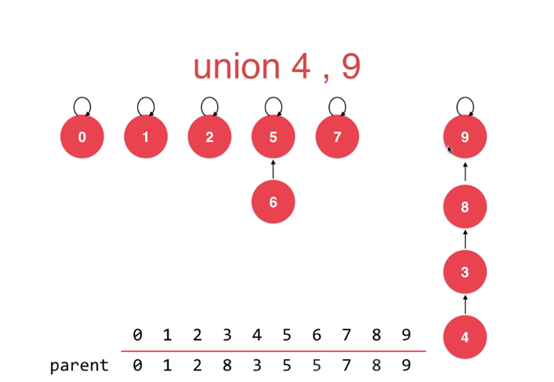
我们来看最终的并查集两种不同的显示结果

相信可以很快的看出结果。

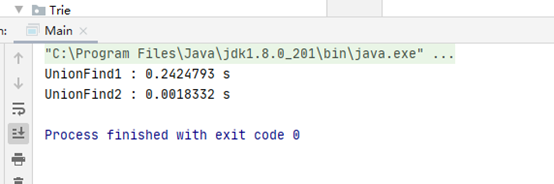
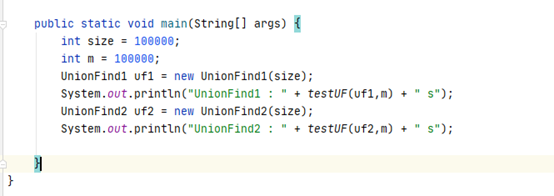
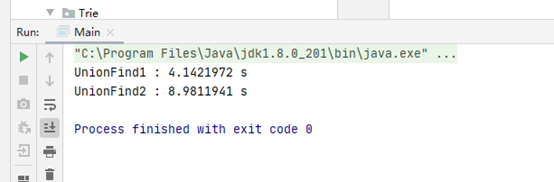
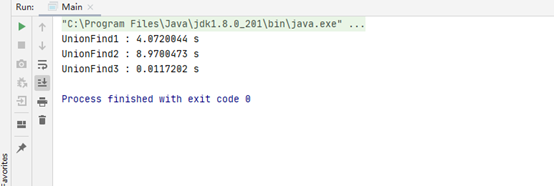
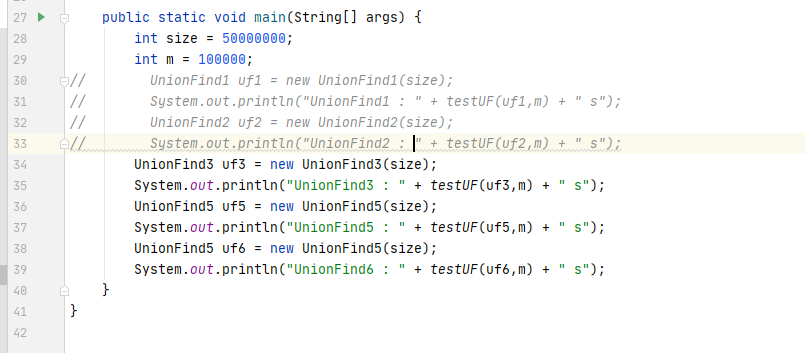
测试一下

温馨提示

可以看到时间的差异化，虽然这个测试并不是特别的规范。

当我们将操作变大

可以看到树居然会更慢了

温馨提示

这里有一个原因是在数组中，数组底层会有很多的优化，我们的树依然也是可以有很多的优化的。
这里一个简单的解决方案：考虑size
我们看下面的一个例子：现在我们要把4合并到9，我们合并前是这个样子

温馨提示

合并之后是这个样子，树的高度由3变成了4，这样我们就变得复杂了，那我们有没有一种好办法呢？

结论

我们可以让9指向8，这样我们的数高度还是3，并没有增加，因为我们知道如果我们一直使用之前我们用的那种方法，我们的这个并查集有可能会退化为一个链表，这种是非常不友好的，具体主要如下图：

这种的优化思路是非常简单的，让我们来看一下具体的代码实现：

package UnionFind;

/**
 * 优化第一版的树
 */
public class UnionFind3 implements UF {
    private int[] parent;
    private int[] sz; //sz[i] 表示为以i为根的集合中元素个数

    public UnionFind3(int size) {

        parent = new int[size];
        sz = new int[size];
        for (int i = 0; i < size; i++) {
            parent[i] = i;
            sz[i] = 1;
        }
    }

    @Override
    public int getSize() {
        return parent.length;
    }

    // 查找过程，查找元素p所对应的集合编号
    // O（h）复杂度，h为树的高度
    private int find(int p) {
        while (p != parent[p]) {
            p = parent[p];
        }
        return p;
    }

    // 查看元素p和元素q是否所属一个集合
    // O(h)复杂度，h为树的高度
    @Override
    public boolean isConnected(int p, int q) {

        return find(p) == find(q);
    }

    // 合并元素p和元素q所属的集合
    // O（h）复杂度，h为树的高度
    @Override
    public void unionElements(int p, int q) {
        int pRoot = find(p);
        int qRoot = find(q);
        if (pRoot == qRoot) {
            return;
        }
        // 根据两个元素所在树的元素个数不同判断合并方向
        // 将元素个数少的集合合并到元素个数多的集合上
        if (sz[pRoot] < sz[qRoot]) {
            parent[pRoot] = qRoot;
            sz[qRoot] += sz[pRoot];
        } else {
            // sz[qRoot] <= sz[pRoot]
            parent[qRoot] = pRoot;
            sz[pRoot] += sz[qRoot];
        }
    }
}

优化过后

效果是非常惊人的！

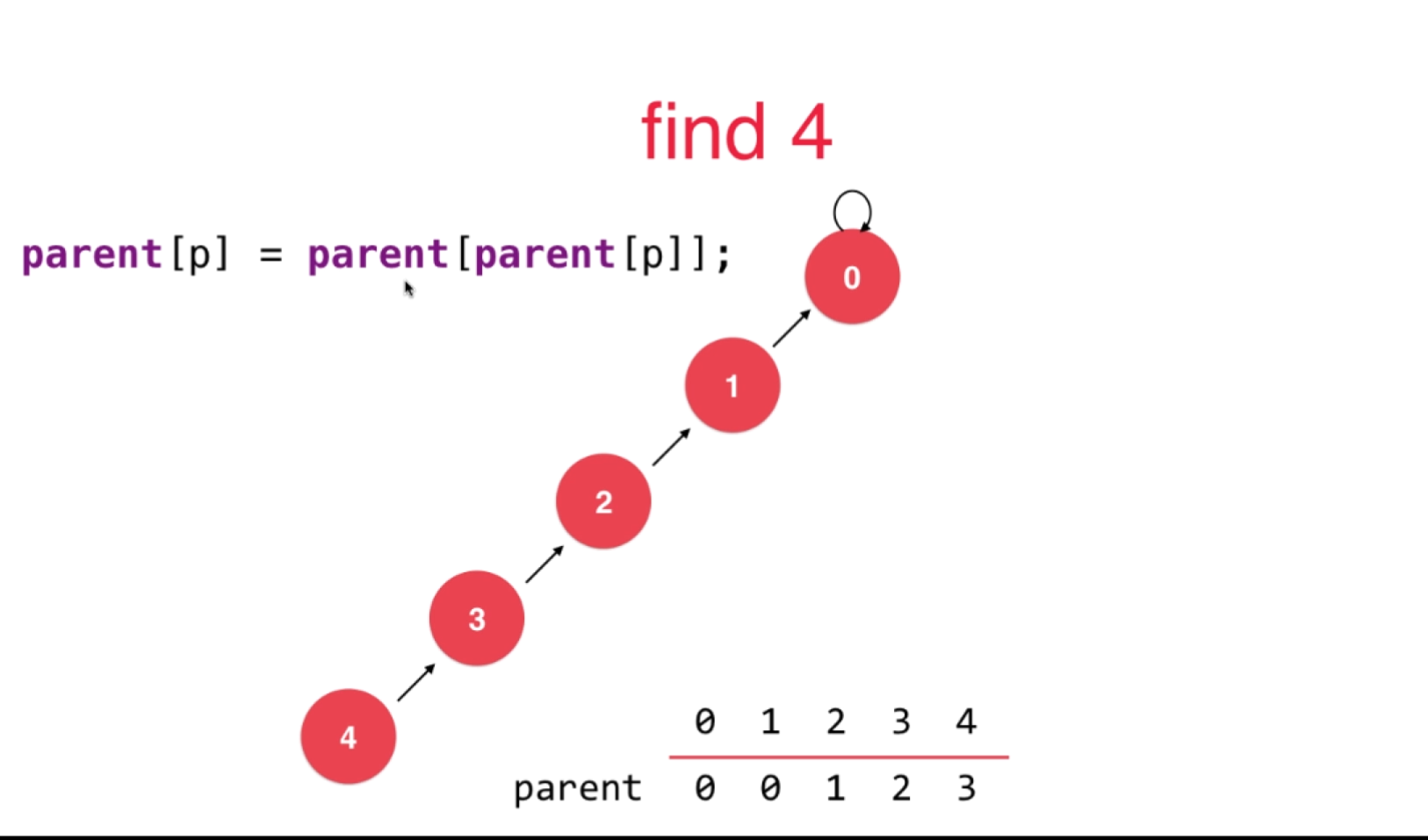
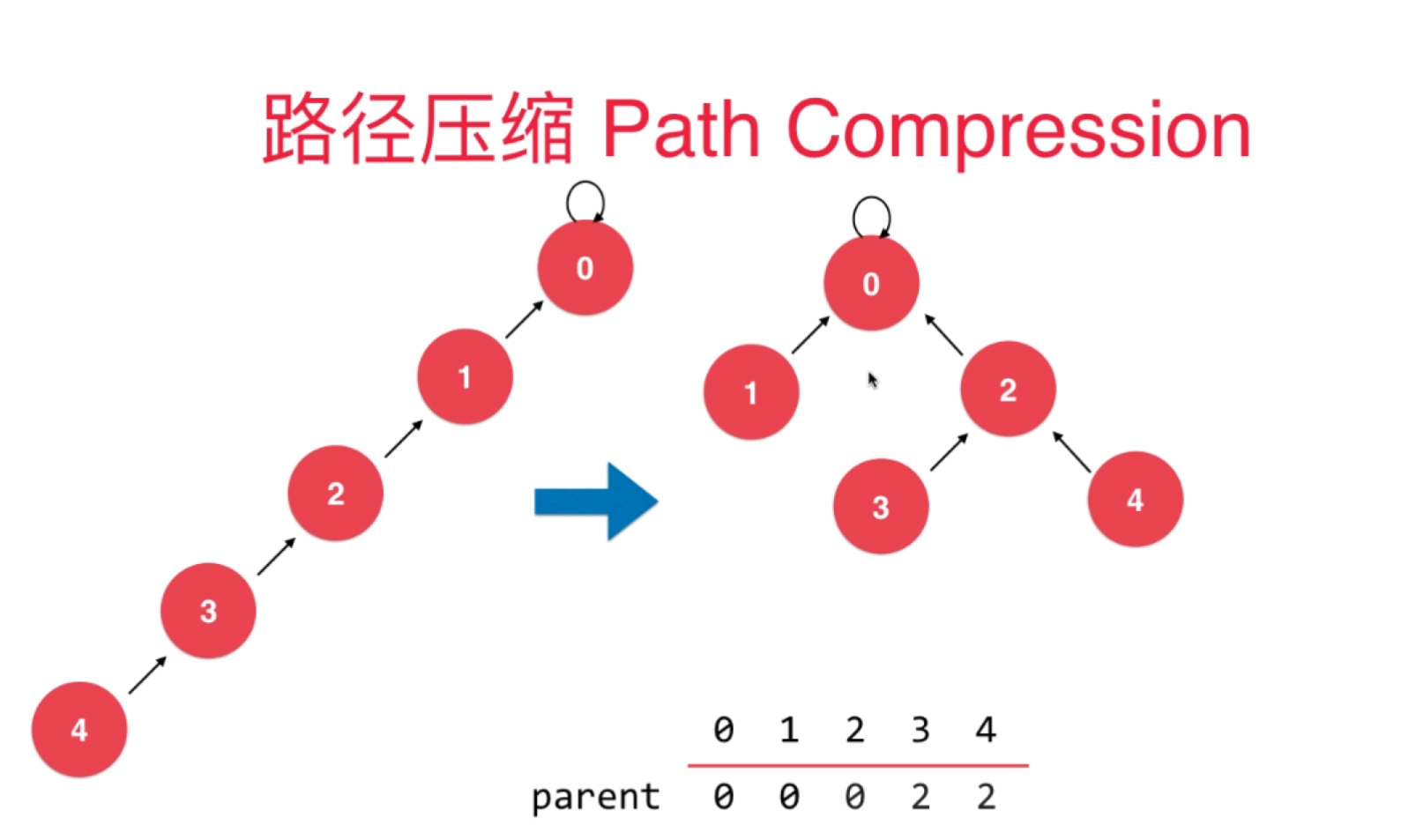
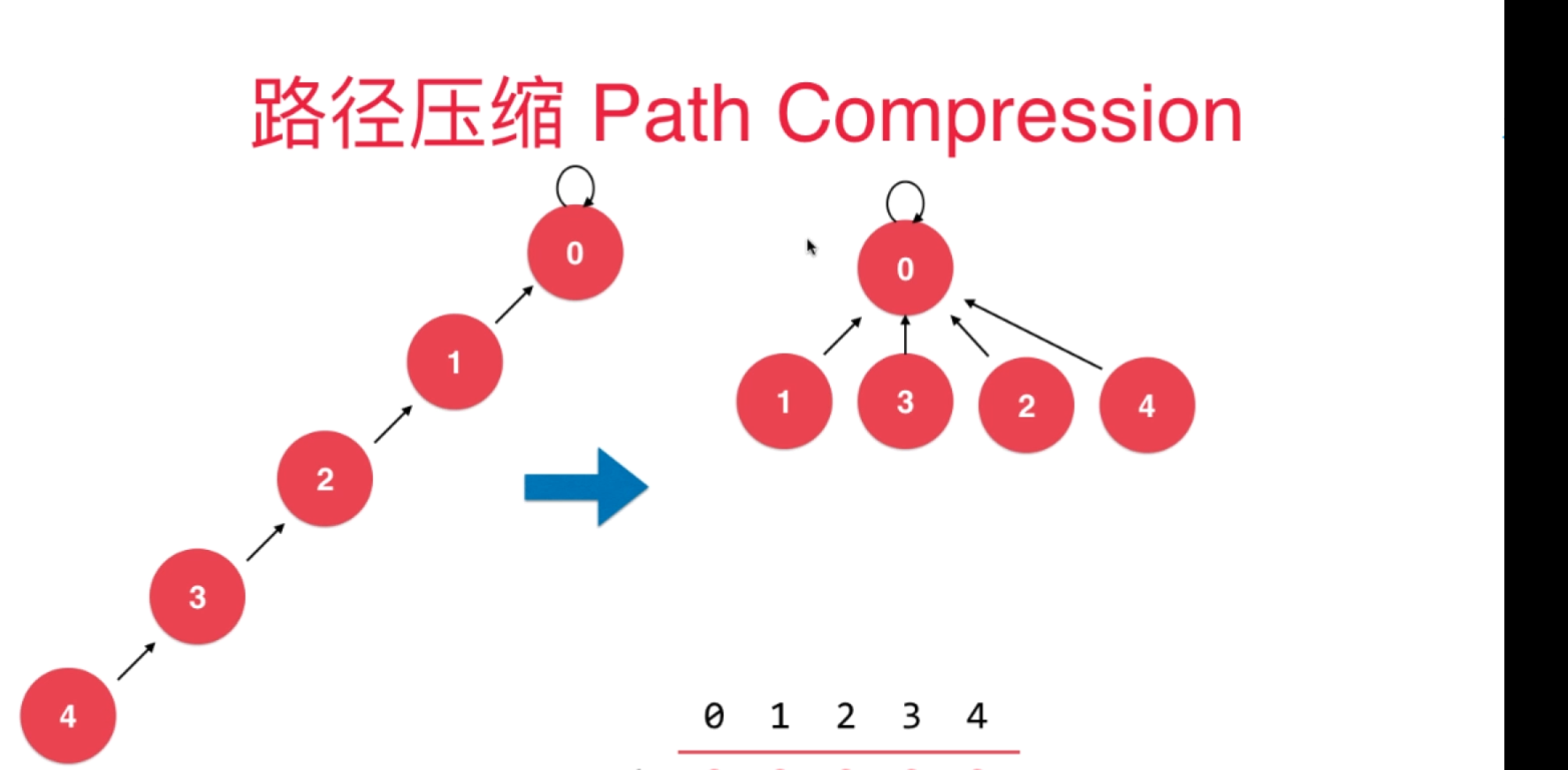
四、路径压缩

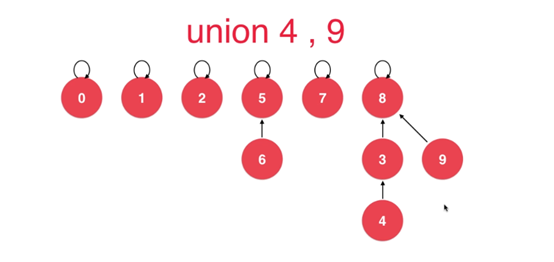
看两张图，清晰可知

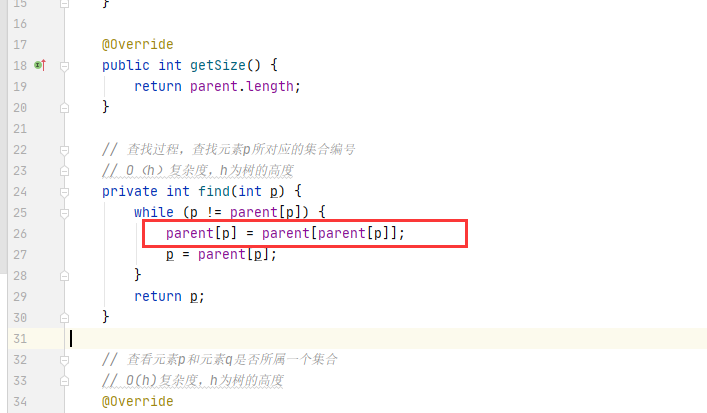
代码实现

    // 查找过程，查找元素p所对应的集合编号
    // O（h）复杂度，h为树的高度
    private int find(int p) {
        while (p != parent[p]) {
            parent[p] = parent[parent[p]];
            p = parent[p];
        }
        return p;
    }

仅仅一行代码

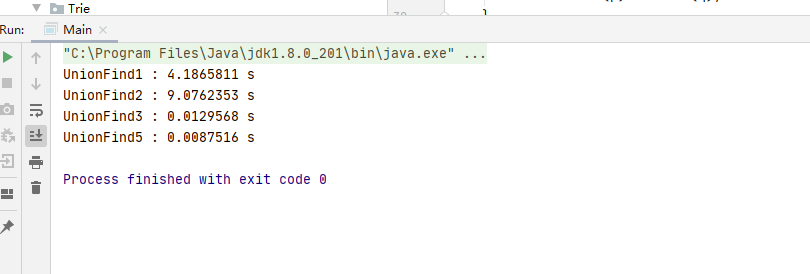
结果如下

五、对并查集继续优化

我们可不可以直接优化成下面这种直接指向根节点的情况呢？

代码实现

    // 查找过程，查找元素p所对应的集合编号
    // O（h）复杂度，h为树的高度
    private int find(int p) {
        if (p != parent[p]) {
            parent[p] = find(parent[p]);
        }
        return p;
    }

测试一下

六、并查集的时间复杂度