线段树

DBC 2.3K 0

一、什么是线段树

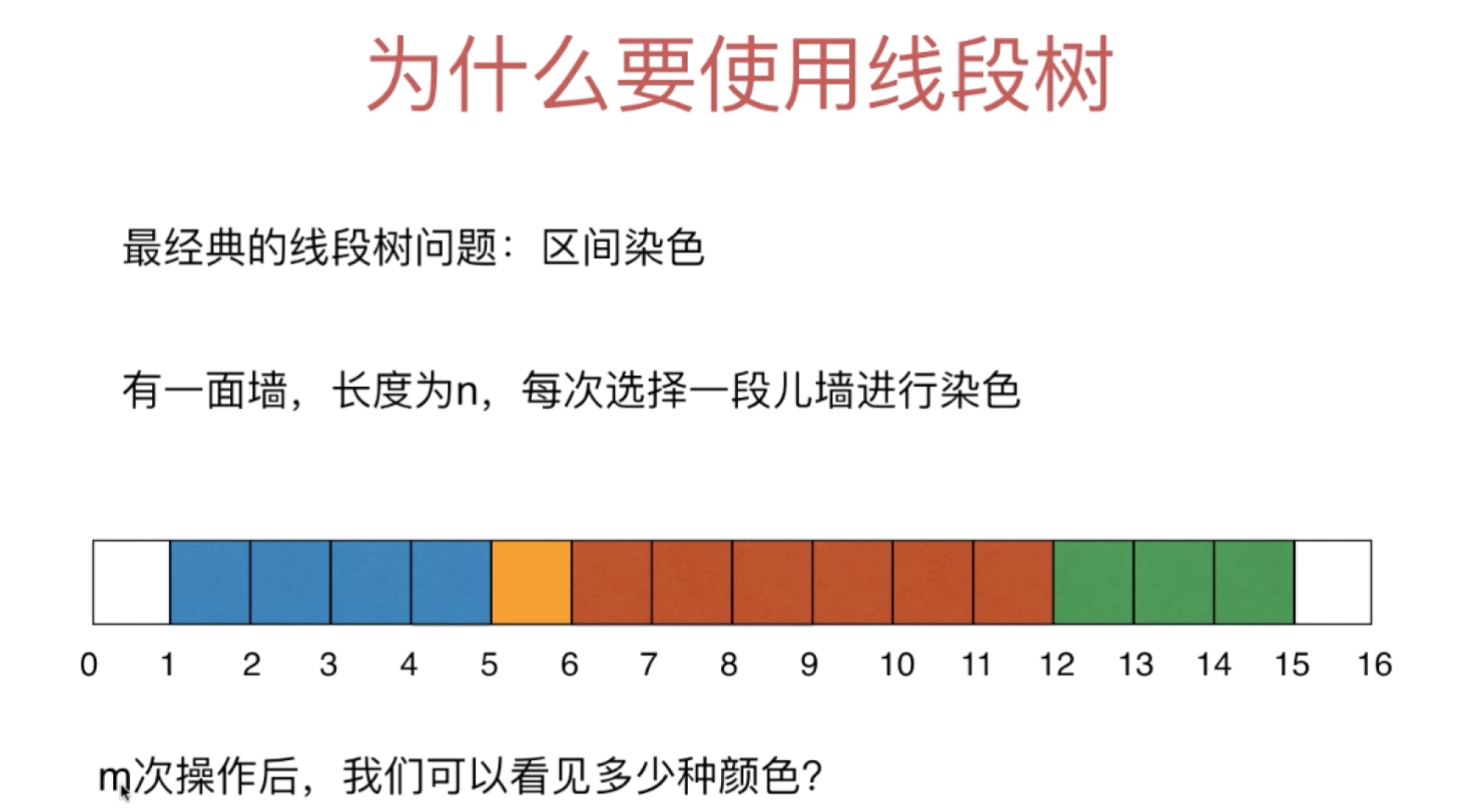
为什么要使用线段树

  • 最经典的线段树问题：区间染色
    • 有一段墙，长度为n，每次选择一段儿墙进行染色

    • 线段树插图

    • m次操作后，我们可以在[ i , j ] 区间内看见多少种颜色 （使用数组实现）
      • 染色操作（更新区间）
        • O （n）
      • 查询操作（查询区间）
        • O （n）
  • 另一类经典问题：区间查询

    • 线段树插图2

    • 查询一个区间 [ i , j ] 的最大值，最小值，或者区间数字和
      • 实质：基于区间的统计查询
    • 小例子：
      • 2017年注册用户中消费最高的用户 ?   消费最少的用户 ？  学习时间最长的用户 ？
      • 某个太空区间中天体总量 ？
  • 总结：以上例子都可以使用数组实现：
    • 更新
      • 使用数组实现
        • O（n）
      • 使用线段树实现
        • O（logn）
    • 查询
      • 使用数组实现
        • O（n）
      • 使用线段树实现
        • O（logn）

线段树的力量

线段树插图4

 

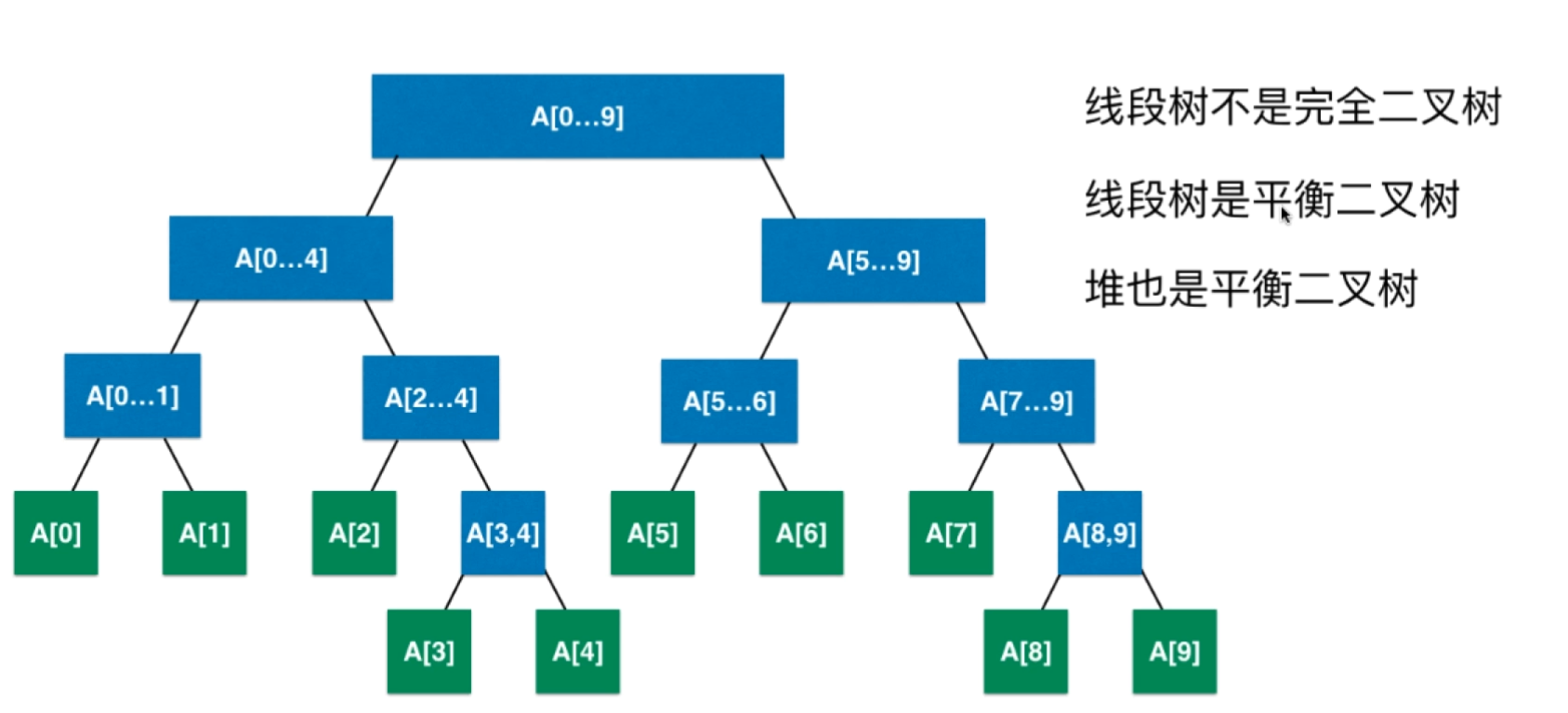
二、线段树基础表示

线段树插图6

  • 如果区间有n个元素 数组表示需要有多少节点？
    • 需要 4n 的空间
  • 我们的线段树不考虑添加元素，即区间固定
    • 使用 4n 的静态空间即可

初步实现

import java.util.Objects;

/**
 * @author DBC
 * @version 1.0
 * @date 2022-02-15 21:25
 */
public class SegmentTree<E> {
    private E[] tree;
    private E[] data;

    public SegmentTree(E[] arr) {
        data = (E[]) new Object[arr.length];
        for (int i = 0; i < arr.length; i++) {
            data[i] = arr[i];
        }
        tree = (E[]) new Object[4 * arr.length];
    }

    public int getSize() {
        return data.length;
    }

    public E get(int index) {
        if (index < 0 || index >= data.length) {
            throw new IllegalArgumentException("Index is illegal.");
        }
        return data[index];
    }
    // 返回完全二叉树的数组表示中，一个索引所表示的元素的左孩子节点的索引
    private int leftChild(int index){
        return 2 * index + 1;
    }

    // 返回完全二叉树的数组表示中，一个索引所表示的元素的右孩子节点的索引
    private int rightChild(int index){
        return 2 * index + 2;
    }
}

三、创建线段树

package SegmentTree;

import java.util.Objects;

/**
 * @author DBC
 * @version 1.0
 * @date 2022-02-15 21:25
 */
public class SegmentTree<E> {
    private E[] tree;
    private E[] data;
    private Merger<E> merger;

    public SegmentTree(E[] arr, Merger<E> merger) {
        this.merger = merger;
        data = (E[]) new Object[arr.length];
        for (int i = 0; i < arr.length; i++) {
            data[i] = arr[i];
        }
        tree = (E[]) new Object[4 * arr.length];
        buildSegmentTree(0, 0, data.length - 1);
    }

    // 在treeIndex的位置创建表示区间 [ l...r ]的线段树
    private void buildSegmentTree(int treeIndex, int l, int r) {
        if (l == r) {
            tree[treeIndex] = data[l];
            return;
        }
        int leftTreeIndex = leftChild(treeIndex);
        int rightTreeindex = rightChild(treeIndex);

        int mid = l + (r - l) / 2; //可以避免两个相加过大 导致的整形溢出
        buildSegmentTree(leftTreeIndex, l, mid);
        buildSegmentTree(rightTreeindex, mid + 1, r);

        tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeindex]);
    }

    public int getSize() {
        return data.length;
    }

    public E get(int index) {
        if (index < 0 || index >= data.length) {
            throw new IllegalArgumentException("Index is illegal.");
        }
        return data[index];
    }

    // 返回完全二叉树的数组表示中，一个索引所表示的元素的左孩子节点的索引
    private int leftChild(int index) {
        return 2 * index + 1;
    }

    // 返回完全二叉树的数组表示中，一个索引所表示的元素的右孩子节点的索引
    private int rightChild(int index) {
        return 2 * index + 2;
    }

    @Override
    public String toString() {
        StringBuilder res = new StringBuilder();
        res.append("[");
        for (int i = 0; i < tree.length; i++) {
            if (tree[i] != null) {
                res.append(tree[i]);
            } else {
                res.append("null");
            }
            if (i != tree.length - 1) {
                res.append(", ");
            }

        }
        res.append("]");

        return res.toString();
    }
}

package SegmentTree;

/**
 * @author DBC
 * @version 1.0
 * @date 2022-02-15 21:41
 */
public interface Merger<E> {
    E merge(E a, E b);
}

测试一下

/**
 * @author DBC
 * @version 1.0
 * @date 2022-02-15 21:44
 */
public class Main {
    public static void main(String[] args) {
        Integer[] nums = {-2, 0, 3, -5, 2, -1};
        SegmentTree<Integer> segTree = new SegmentTree<Integer>(nums, new Merger<Integer>() {
            @Override
            public Integer merge(Integer a, Integer b) {
                return a + b;
            }
        });

        SegmentTree<Integer> segTree2 = new SegmentTree<Integer>(nums, (a, b) -> a + b);

        System.out.println(segTree);
        System.out.println(segTree2);
    }
}

线段树插图8

四、线段树中的区间查询

关键代码

    // 返回区间 [ queryL , queryR ] 的值
    public E query(int queryL, int queryR) {
        if (queryL < 0 || queryL >= data.length || queryR < 0 || queryR >= data.length || queryL > queryR) {
            throw new IllegalArgumentException("Index is illegal");
        }
        return query(0, 0, data.length - 1, queryL, queryR);
    }

    // 在以treeID为根的线段树中 [l...r]的范围里，搜索区间 [queryL ... queryR] 的值
    public E query(int treeIndex, int l, int r, int queryL, int queryR) {
        if (l == queryL && r == queryR) {
            return tree[treeIndex];
        }
        int mid = l + (r - l) / 2;
        int leftTreeIndex = leftChild(treeIndex);
        int rightTreeIndex = rightChild(treeIndex);
        if (queryL >= mid + 1) {
            return query(rightTreeIndex, mid + 1, r, queryL, queryR);
        } else if (queryR <= mid) {
            return query(leftTreeIndex, l, mid, queryL, queryR);
        }
        E leftResult = query(leftTreeIndex, l, mid, queryL, mid);
        E rightResult = query(rightTreeIndex, mid + 1, r, mid + 1, queryR);
        return merger.merge(leftResult,rightResult);
    }

、

测试一下

/**
 * @author DBC
 * @version 1.0
 * @date 2022-02-15 21:44
 */
public class Main {
    public static void main(String[] args) {
        Integer[] nums = {-2, 0, 3, -5, 2, -1};
//        SegmentTree<Integer> segTree = new SegmentTree<Integer>(nums, new Merger<Integer>() {
//            @Override
//            public Integer merge(Integer a, Integer b) {
//                return a + b;
//            }
//        });

        SegmentTree<Integer> segTree2 = new SegmentTree<Integer>(nums, (a, b) -> a + b);

        System.out.println(segTree2.query(0,1));
        System.out.println(segTree2.query(2,5));
        System.out.println(segTree2.query(0,5));
//        System.out.println(segTree2);
    }
}

线段树插图10

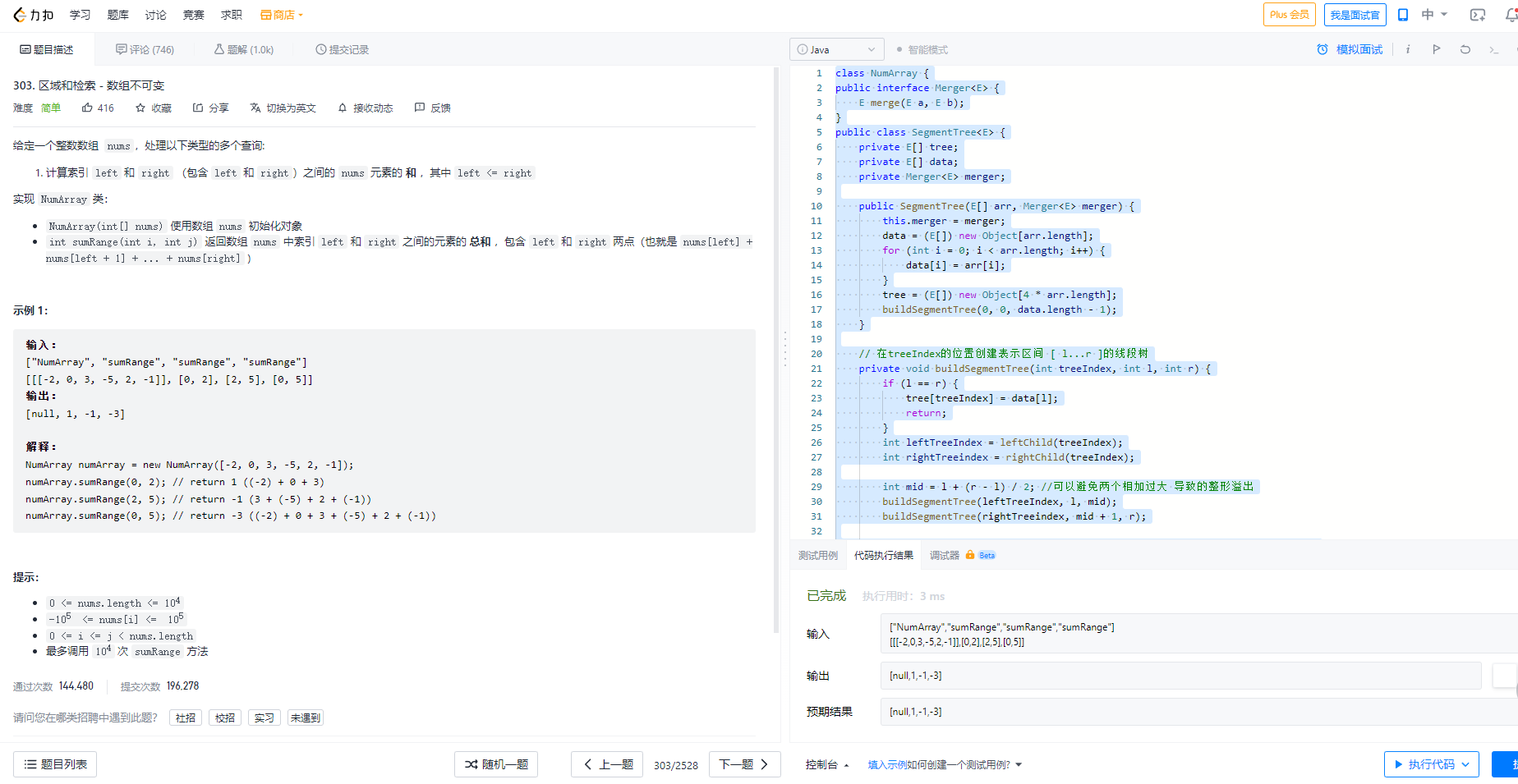
五、Leetcode上线段树相关的问题

线段树插图12

class NumArray {
public interface Merger<E> {
    E merge(E a, E b);
}
public class SegmentTree<E> {
    private E[] tree;
    private E[] data;
    private Merger<E> merger;

    public SegmentTree(E[] arr, Merger<E> merger) {
        this.merger = merger;
        data = (E[]) new Object[arr.length];
        for (int i = 0; i < arr.length; i++) {
            data[i] = arr[i];
        }
        tree = (E[]) new Object[4 * arr.length];
        buildSegmentTree(0, 0, data.length - 1);
    }

    // 在treeIndex的位置创建表示区间 [ l...r ]的线段树
    private void buildSegmentTree(int treeIndex, int l, int r) {
        if (l == r) {
            tree[treeIndex] = data[l];
            return;
        }
        int leftTreeIndex = leftChild(treeIndex);
        int rightTreeindex = rightChild(treeIndex);

        int mid = l + (r - l) / 2; //可以避免两个相加过大 导致的整形溢出
        buildSegmentTree(leftTreeIndex, l, mid);
        buildSegmentTree(rightTreeindex, mid + 1, r);

        tree[treeIndex] = merger.merge(tree[leftTreeIndex], tree[rightTreeindex]);
    }

    public int getSize() {
        return data.length;
    }

    public E get(int index) {
        if (index < 0 || index >= data.length) {
            throw new IllegalArgumentException("Index is illegal.");
        }
        return data[index];
    }

    // 返回完全二叉树的数组表示中，一个索引所表示的元素的左孩子节点的索引
    private int leftChild(int index) {
        return 2 * index + 1;
    }

    // 返回完全二叉树的数组表示中，一个索引所表示的元素的右孩子节点的索引
    private int rightChild(int index) {
        return 2 * index + 2;
    }

    // 返回区间 [ queryL , queryR ] 的值
    public E query(int queryL, int queryR) {
        if (queryL < 0 || queryL >= data.length || queryR < 0 || queryR >= data.length || queryL > queryR) {
            throw new IllegalArgumentException("Index is illegal");
        }
        return query(0, 0, data.length - 1, queryL, queryR);
    }

    // 在以treeID为根的线段树中 [l...r]的范围里，搜索区间 [queryL ... queryR] 的值
    public E query(int treeIndex, int l, int r, int queryL, int queryR) {
        if (l == queryL && r == queryR) {
            return tree[treeIndex];
        }
        int mid = l + (r - l) / 2;
        int leftTreeIndex = leftChild(treeIndex);
        int rightTreeIndex = rightChild(treeIndex);
        if (queryL >= mid + 1) {
            return query(rightTreeIndex, mid + 1, r, queryL, queryR);
        } else if (queryR <= mid) {
            return query(leftTreeIndex, l, mid, queryL, queryR);
        }
        E leftResult = query(leftTreeIndex, l, mid, queryL, mid);
        E rightResult = query(rightTreeIndex, mid + 1, r, mid + 1, queryR);
        return merger.merge(leftResult,rightResult);
    }

    @Override
    public String toString() {
        StringBuilder res = new StringBuilder();
        res.append("[");
        for (int i = 0; i < tree.length; i++) {
            if (tree[i] != null) {
                res.append(tree[i]);
            } else {
                res.append("null");
            }
            if (i != tree.length - 1) {
                res.append(", ");
            }

        }
        res.append("]");

        return res.toString();
    }
}
    private SegmentTree<Integer> segmentTree;

    public NumArray(int[] nums) {
        if (nums.length > 0) {
            Integer[] data = new Integer[nums.length];
            for (int i = 0; i < nums.length; i++) {
                data[i] = nums[i];
            }
            segmentTree = new SegmentTree<Integer>(data, (a, b) -> a + b);
        }
    }

    int sumRange(int left, int right) {
        if (segmentTree == null) {
            throw new IllegalArgumentException("Segment Tree is null");
        }
        return segmentTree.query(left, right);
    }
}

/**
 * Your NumArray object will be instantiated and called as such:
 * NumArray obj = new NumArray(nums);
 * int param_1 = obj.sumRange(left,right);
 */

换一种方式实现

/**
 * @author DBC
 * @version 1.0
 * @date 2022-02-16 21:33
 */
public class NumArray2 {

    private int[] sum; // sum[i]存储前i个元素和，sum[0] = 0
                       // sum[i]存储nums[0...i-1]的和
    public NumArray2(int[] nums) {
        sum = new int[nums.length+1];
        sum[0] = 0;
        for (int i=1;i<sum.length;i++){
            sum[i] = sum[i-1] + nums[i-1];
        }
    }

    public int sumRange(int i, int j) {
        return sum[j+1] - sum[i];
    }
}

线段树插图14

本文作者为DBC，转载请注明。

发表评论 取消回复
表情 图片 链接 代码

分享