基于比较排序算法大总结

七个排序算法的小总结

• 选择排序法
  • 时间：O（n²）
  • 空间：O（1）
• 插入排序法
  • 时间：O（n²）
  • 空间：O（1）
  • 完全有序的数组，时间O（n）
• 冒泡排序法
  • 时间：O（n²）
  • 空间：O（1）
  • 完全有序的数组，时间O（n）
• 归并排序法
  • 时间：O（nlogn）
  • 空间：O（n）
  • 完全有序的数组，时间O（n）
  • O（nlogn） 求解数组中逆序对个数
• 快速排序法
  • 时间：O（nlogn）
  • 空间：O（1）
  • 含有相同元素数组，三路快排时间O（n）
  • O（n） 求解selectK，topK 问题
• 堆排序法
  • 时间：O（nlogn）
  • 空间：O（1）
  • 堆，优先队列
• 希尔排序法
  • 时间：O（nlogn）- O（n²）
  • 空间：O（1）
  • 分组的思想

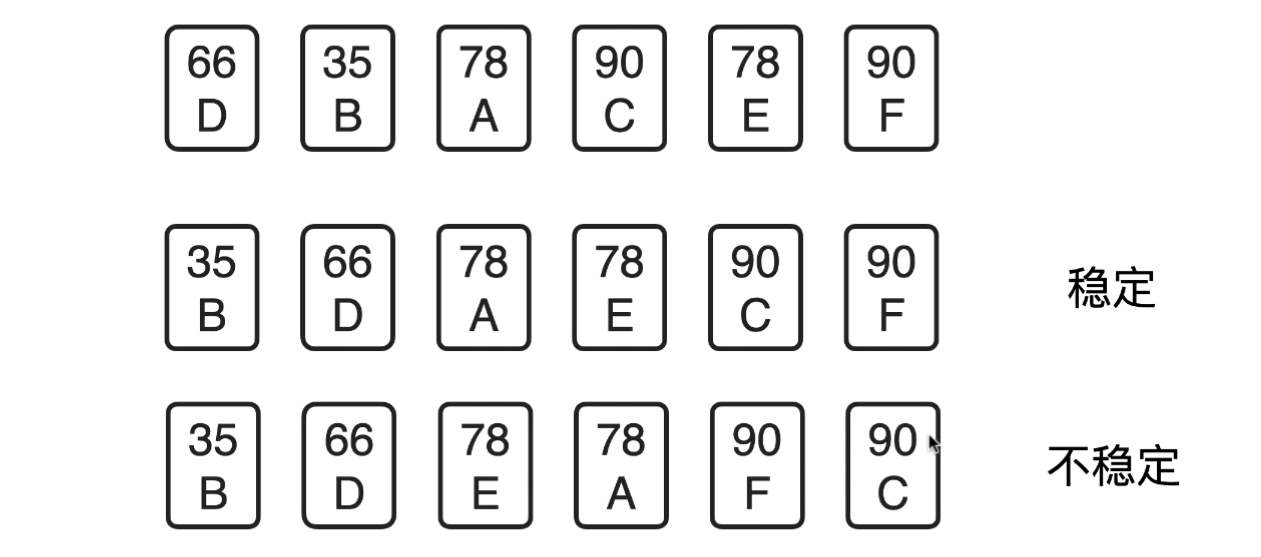
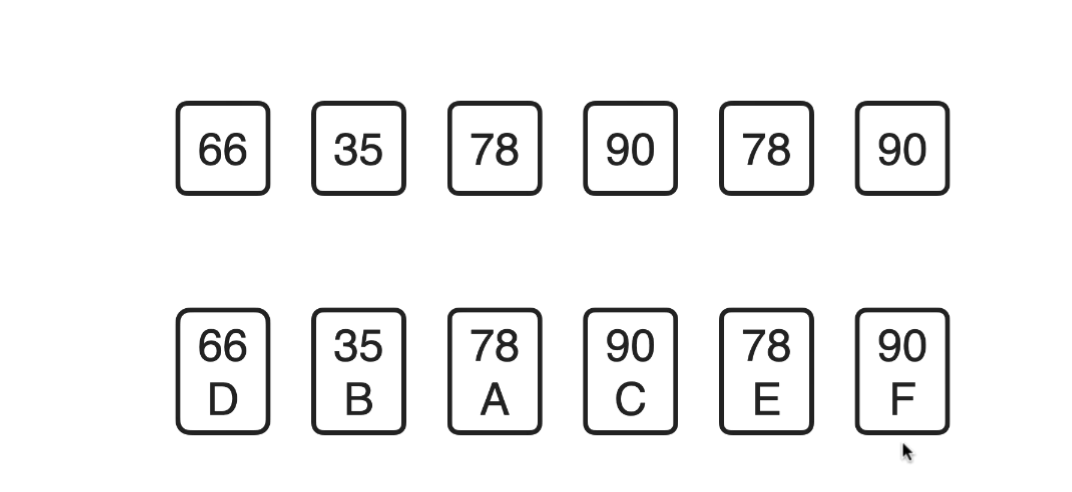
二、排序算法的稳定性

排序的稳定性：排序前相等的两个元素，排序后相对不变

温馨提示

如果我们每一次都能获得第二种的排序，那么我们就称这种为稳定的排序算法 [aru_67]

• 选择排序法是不稳定的
  • 可能被实现成不稳定的排序算法
• 插入排序是稳定的
  • 相同大小没有机会“跳跃”
  • 依赖具体实现

  • 

    • 注意标红的 <（小于） 号，如果我们写 ≤ 那么就会变成不稳定，相信小伙伴很容易理解[aru_51]
• 希尔排序是不稳定的
• 冒泡排序是稳定的
  • 每次只比较相邻元素
  • 相同大小的元素没有机会“跳跃”

  • 

  • 和上面插入排序算法同理，就不说那么多了 [aru_36]

三、高级排序算法的稳定性

• 快速排序法师不稳定的
  • 随机化标定点直接打乱了顺序
• 堆排序法师不稳定的
• 归并排序法是稳定的
  • 归并排序的元素位置移动，完全在 merge 的过程中
  • 归并过程中，相同元素没有机会“跳”到前面去
  • 

如果元素只有一个域，稳定性没有意义

温馨提示

就像上面那个，数组，你要来说数组的稳定性，那是完全没有意义的，只有第二个数组才会有意义！懂的都懂！ [aru_53]
举一个例子：学生的排名通过姓名进行排序，然后现在我们需要通过分数进行排序，如果我们的排序算法不是稳定的，那么在排序之后，学生的之前通过姓名排序的结果就会被打乱，那么肯定是不符合我们的要求的！相信懂的都懂！

所以我们需要一个稳定的排序算法来实现我们的这个需求！ [aru_43]

看一个图片例子：

我们可以在排序的时候再加上一个条件来判断，这样会对性能有那么一点点的消耗，但是在现在的企业开发中，这种微末的性能损耗，一般都是忽略不计的，因为只是简单的判断，如果企业中对性能的要求非常非常的高，一点点损耗都不能浪费，那么我们这里就推荐使用稳定的排序算法了，也就是——归并排序法了 [aru_50]