一、什么是优先队列
二、堆的基础表示
package MaxHeap;
import List.Array;
public class MaxHeap<E extends Comparable<E>> {
private Array<E> data;
public MaxHeap(int capacity) {
data = new Array<>(capacity);
}
public MaxHeap() {
data = new Array<>();
}
// 返回堆中的元素个数
public int size() {
return data.getSize();
}
// 返回一个布尔值,表示堆中是否为空
public boolean isEmpty() {
return data.isEmpty();
}
// 返回完全二叉树的数组表示中,一个索引所表示的元素的父亲节点的索引
public int parent(int index) {
if (index == 0) {
throw new IllegalArgumentException("index-0 doesmn`t have parent.");
}
return (index - 1) / 2;
}
//返回完全二叉树的数组表示中,一个索引所表示的元素的左孩子节点的索引
private int leftChild(int index) {
return index * 2 + 1;
}
//返回完全二叉树的数组表示中,一个索引所表示的元素的右孩子节点的索引
private int rightChild(int index) {
return index * 2 + 2;
}
}
三、向堆中添加元素和Sift Up
// 向堆中添加元素
public void add(E e) {
data.addLast(e);
siftUp(data.getSize() - 1);
}
private void siftUp(int k) {
while (k > 0 && data.get(parent(k)).compareTo(data.get(k)) < 0) {
data.swap(k, parent(k));
k = parent(k);
}
} 四、从堆中取出元素和Sift Down
// 看堆中的最大元素
public E findMax() {
if (data.getSize() == 0) {
throw new IllegalArgumentException("数组为空!");
}
return data.get(0);
}
// 取出堆中最大元素
public E extractMax() {
E ret = findMax();
data.swap(0, data.getSize() - 1);
data.removeLast();
siftDown(0);
return ret;
}
private void siftDown(int k) {
while (leftChild(k) < data.getSize()) {
int j = leftChild(k);
if (j + 1 < data.getSize() && data.get(j + 1).compareTo(data.get(j)) > 0) {
j = rightChild(k);
}
// data[j] 是 leftChild 和 rightChild 中的最大值
if (data.get(k).compareTo(data.get(j)) >= 0) {
break;
}
data.swap(k, j);
k = j;
}
}
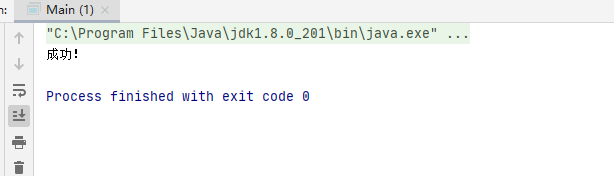
测试一下
public class Main {
public static void main(String[] args) {
int n = 1000000;
MaxHeap<Integer> maxHeap = new MaxHeap<Integer>();
Random random = new Random();
for (int i = 0; i < n; i++) {
maxHeap.add(random.nextInt(Integer.MAX_VALUE));
}
int[] arr = new int[n];
for (int i = 0; i < n; i++) {
arr[i] = maxHeap.extractMax();
}
for (int i = 1; i < n; i++) {
if (arr[i - 1] < arr[i]) {
throw new IllegalArgumentException("报错了");
}
}
System.out.println("成功!");
}
}
五、最直观的堆排序
简单实现加测试
import MergeSort.ArrayGenerator;
import MergeSort.SortingHelper;
import java.util.Arrays;
public class HeapSort {
private HeapSort() {
}
public static <E extends Comparable<E>> void sort(E[] data) {
MaxHeap<E> maxHeap = new MaxHeap<E>();
for (E e : data) {
maxHeap.add(e);
}
for (int i = data.length - 1; i >= 0; i--) {
data[i] = maxHeap.extractMax();
}
}
public static void main(String[] args) {
int n = 1000000;
Integer[] arr = ArrayGenerator.generateRandomArray(n,n);
Integer[] arr2 = Arrays.copyOf(arr,arr.length);
Integer[] arr3 = Arrays.copyOf(arr,arr.length);
Integer[] arr4 = Arrays.copyOf(arr,arr.length);
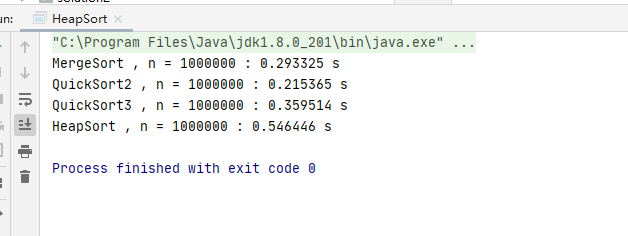
SortingHelper.sortTest("MergeSort",arr);
SortingHelper.sortTest("QuickSort2",arr2);
SortingHelper.sortTest("QuickSort3",arr3);
SortingHelper.sortTest("HeapSort",arr4);
}
}
六、Heapify 和 Replace
- replace:取出最大元素后,放入一个新元素
- 实现:可以先extractMax,再add,两次O(logn)的操作
- 实现:可以直接将堆顶元素替换以后Sift Down,一次O(logn)的操作
// 取出堆中的最大元素,并且替换成元素e
public E replace(E e) {
E ret = findMax();
data.set(0, e);
siftDown(0);
return ret;
} - heapify:将任意数组整理成堆的形状
- 将n个元素逐个插入到一个空堆中,算法复杂度是O(nlogn)
- heapify的过程,算法复杂度为O(n)
七、实现 Heapify
点击查看MaxHeap
package MaxHeap;
import List.Array;
public class MaxHeap<E extends Comparable<E>> {
private Array<E> data;
public MaxHeap(int capacity) {
data = new Array<>(capacity);
}
public MaxHeap() {
data = new Array<>();
}
public MaxHeap(E[] arr) {
data = new Array<>(arr);
for (int i = parent(arr.length - 1); i >= 0; i--) {
siftDown(i);
}
}
// 返回堆中的元素个数
public int size() {
return data.getSize();
}
// 返回一个布尔值,表示堆中是否为空
public boolean isEmpty() {
return data.isEmpty();
}
// 返回完全二叉树的数组表示中,一个索引所表示的元素的父亲节点的索引
public int parent(int index) {
if (index == 0) {
throw new IllegalArgumentException("index-0 doesmn`t have parent.");
}
return (index - 1) / 2;
}
//返回完全二叉树的数组表示中,一个索引所表示的元素的左孩子节点的索引
private int leftChild(int index) {
return index * 2 + 1;
}
//返回完全二叉树的数组表示中,一个索引所表示的元素的右孩子节点的索引
private int rightChild(int index) {
return index * 2 + 2;
}
// 向堆中添加元素
public void add(E e) {
data.addLast(e);
siftUp(data.getSize() - 1);
}
private void siftUp(int k) {
while (k > 0 && data.get(parent(k)).compareTo(data.get(k)) < 0) {
data.swap(k, parent(k));
k = parent(k);
}
}
// 看堆中的最大元素
public E findMax() {
if (data.getSize() == 0) {
throw new IllegalArgumentException("数组为空!");
}
return data.get(0);
}
// 取出堆中最大元素
public E extractMax() {
E ret = findMax();
data.swap(0, data.getSize() - 1);
data.removeLast();
siftDown(0);
return ret;
}
private void siftDown(int k) {
while (leftChild(k) < data.getSize()) {
int j = leftChild(k);
if (j + 1 < data.getSize() && data.get(j + 1).compareTo(data.get(j)) > 0) {
j = rightChild(k);
}
// data[j] 是 leftChild 和 rightChild 中的最大值
if (data.get(k).compareTo(data.get(j)) >= 0) {
break;
}
data.swap(k, j);
k = j;
}
}
// 取出堆中的最大元素,并且替换成元素e
public E replace(E e) {
E ret = findMax();
data.set(0, e);
siftDown(0);
return ret;
}
}
点击查看Array
package List;
import java.util.Objects;
public class Array<E> {
private E[] data;
private int size;
// 构造函数,传入数组的容量capacity构造Array
public Array(int capacity) {
data = (E[]) new Object[capacity];
size = 0;
}
public Array(E[] arr){
data = (E[]) new Object[arr.length];
for (int i=0;i<arr.length;i++){
data[i] = arr[i];
}
size = arr.length;
}
// 无参数的构造函数,默认数组的容量capacity = 10
public Array() {
this(10);
}
// 获取数组中的元素个数
public int getSize() {
return size;
}
// 获取数组的容量
public int getCapacity() {
return data.length;
}
// 数组是否为空
public boolean isEmpty() {
return size == 0;
}
// 向所有元素后添加一个新元素
public void addLast(E e) {
add(size, e);
}
//在所有元素前添加一个元素
public void addFirst(E e) {
add(0, e);
}
// 在第index个位置插入一个新元素e
public void add(int index, E e) {
if (index < 0 || index > size)
System.out.println("添加新元素方法失败,插入位置不可以为负数,也不可以大于数组长度");
if (size == data.length)
resize(2 * data.length);
for (int i = size - 1; i >= index; i--) {
data[i + 1] = data[i];
}
data[index] = e;
size++;
}
// 扩容两倍
private void resize(int newCapacity) {
E[] newData = (E[]) new Object[newCapacity];
for (int i = 0; i < size; i++)
newData[i] = data[i];
data = newData;
}
public void swap(int i,int j){
if (i<0||i>=size||j<0||j>=size){
throw new IllegalArgumentException("Index is illegal.");
}
E e = data[i];
data[i] = data[j];
data[j] = e;
}
@Override
public String toString() {
StringBuilder res = new StringBuilder();
res.append(String.format("Array: size = %d , capacity = %d\n", size, data.length));
for (int i = 0; i < size; i++) {
res.append(data[i]);
if (i != size - 1)
res.append(", ");
}
return res.toString();
}
//获取index索引位置的元素
public E get(int index) {
if (index < 0 || index >= size)
System.out.println("传入不合法!");
return data[index];
}
//修改index索引位置的元素为e
public void set(int index, E e) {
if (index < 0 || index >= size)
System.out.println("传入不合法!");
data[index] = e;
}
// 查找数组中是否有元素e
public boolean contains(E e) {
for (int i = 0; i < size; i++) {
if (data[i].equals(e))
return true;
}
return false;
}
//查找数组中元素e所在的索引,如果不存在元素e,则返回-1
public int find(E e) {
for (int i = 0; i < size; i++) {
if (data[i].equals(e))
return i;
}
return -1;
}
//从数组中删除index位置的元素,返回删除的元素
public E remove(int index) {
if (index < 0 || index >= size)
System.out.println("传入不合法!");
E ret = data[index];
for (int i = index + 1; i < size; i++)
data[i - 1] = data[i];
size--;
data[size] = null; //loitering objects != memory leak
//动态减小数组
if (size == data.length / 4 && data.length / 2 !=0)
resize(data.length / 2);
return ret;
}
// 从数组中删除第一个元素,返回删除的元素
public E removeFirst() {
return remove(0);
}
//从数组中删除最后一个元素,返回删除的元素
public E removeLast() {
return remove(size - 1);
}
// 从数组中删除元素e
public void removeElement(E e) {
int index = find(e);
if (index != -1)
remove(index);
}
}
点击查看Main
package MaxHeap;
import java.util.HashMap;
import java.util.Random;
public class Main {
public static double testHeap(Integer[] testData, boolean isHeapify) {
long startTime = System.nanoTime();
MaxHeap<Integer> maxHeap;
if (isHeapify) {
maxHeap = new MaxHeap<Integer>(testData);
} else {
maxHeap = new MaxHeap<Integer>();
for (int num : testData) {
maxHeap.add(num);
}
}
int[] arr = new int[testData.length];
for (int i = 0; i < testData.length; i++) {
arr[i] = maxHeap.extractMax();
}
for (int i = 1; i < testData.length; i++) {
if (arr[i - 1] < arr[i]) {
throw new IllegalArgumentException("报错了");
}
}
System.out.println("成功!");
long endTime = System.nanoTime();
return (endTime - startTime) / 1000000000.0;
}
public static void main(String[] args) {
int n = 10000000;
Random random = new Random();
Integer[] testData = new Integer[n];
for (int i = 0; i < n; i++) {
testData[i] = random.nextInt(Integer.MAX_VALUE);
}
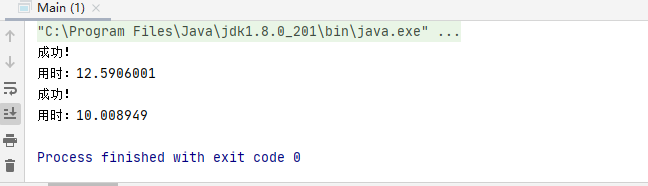
double time1 = testHeap(testData, false);
System.out.println("用时:" + time1);
double time2 = testHeap(testData, true);
System.out.println("用时:" + time2);
}
}
关键代码
public MaxHeap(E[] arr) {
data = new Array<>(arr);
for (int i = parent(arr.length - 1); i >= 0; i--) {
siftDown(i);
}
} public Array(E[] arr){
data = (E[]) new Object[arr.length];
for (int i=0;i<arr.length;i++){
data[i] = arr[i];
}
size = arr.length;
}
本文作者为DBC,转载请注明。