二叉搜索树超级大汇总—

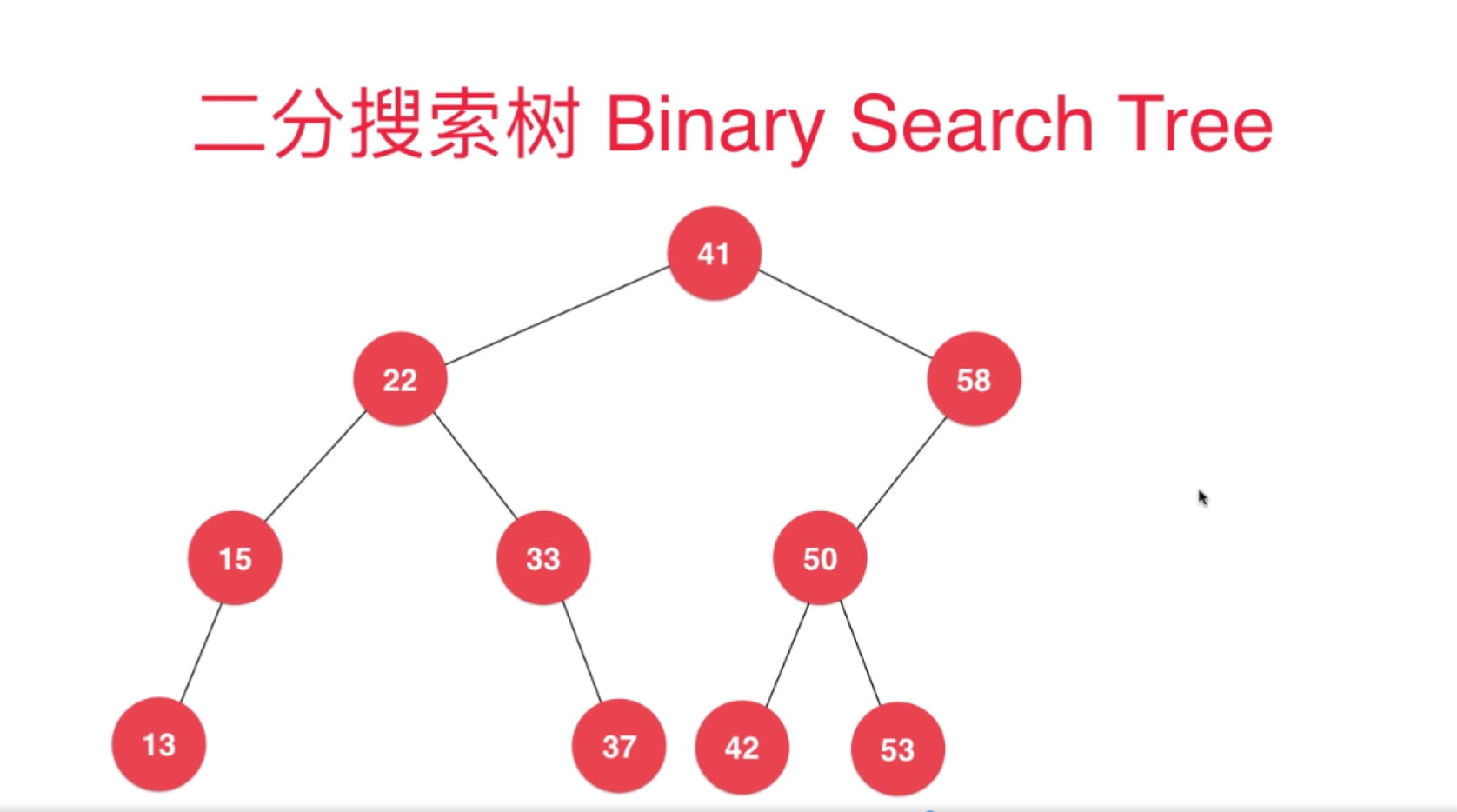
一、二分搜索树 —— Binary Search Tree

二分搜索树是二叉树
二分搜索树的每个节点的值：
- 大于其左子树的所有节点的值
- 小于其右子树的所有节点的值
每一颗子树都是一颗二分搜索树
存储的元素必须有可比较性

二、二分搜索树添加新元素

我们的二分搜索树不包含重复元素
- 如果想包含重复元素，只需要定义：
  - 左子树小于等于节点；或者右子树大于等于节点
- 注意：我们之前讲的数组和链表，可以有重复元素
二分搜索树添加元素的非递归写法，和链表非常的像。
我们这次二分搜索树方面的实现，更多关注递归的实现
在二分搜索树方面，递归的方式比非递归的方式实现起来要简单

详细代码

package bst;

public class BST<E extends Comparable<E>> {
    private class Node {
        public E e;
        public Node left, right;

        public Node(E e) {
            this.e = e;
            left = null;
            right = null;
        }
    }

    private Node root;
    private int size;

    public BST() {
        root = null;
        size = 0;
    }

    public int size() {
        return size;
    }

    public boolean isEmpty() {
        return size == 0;
    }

    // 向二分搜索树中添加新的元素e
    public void add(E e) {
        if (root == null) {
            root = new Node(e);
            size++;
        } else {
            add(root, e);
        }
    }

    // 向以node为根的二分搜索树中插入元素E,递归算法
    private void add(Node node, E e) {
        if (e.equals(node.e)) {
            return;
        } else if (e.compareTo(node.e) < 0 && node.left == null) {
            node.left = new Node(e);
            size++;
            return;
        } else if (e.compareTo(node.e) > 0 && node.right == null) {
            node.right = new Node(e);
            size++;
            return;
        }
        if (e.compareTo(node.e) < 0) {
            add(node.left, e);
        } else {
            // e.compareTo(Node.e) > 0
            add(node.right, e);
        }
    }
}

三、改进add操作，深入了解递归终止函数

温馨提示

我觉得很简单，看看代码就好了，简单的递归而已，不懂的可以带入两个数字进去，模拟流程看看。

关键代码

    // 向二分搜索树中添加新的元素e
    public void add(E e) {

        root = add(root, e);

    }

    // 向以node为根的二分搜索树中插入元素E,递归算法
    // 返回插入新节点后二分搜索树的根
    private Node add(Node node, E e) {

        if (node == null){
            size++;
            return new Node(e);
        }
        if (e.compareTo(node.e) < 0) {
            node.left = add(node.left,e);
        } else if (e.compareTo(node.e)>0){
            // e.compareTo(Node.e) > 0
            node.right = add(node.right,e);
        }
        return node;
    }

四、查找元素

    // 看二分搜索树中是否包含元素e
    public boolean contains(E e) {
        return contains(root, e);
    }

    // 看以node为根的二分搜索树中是否包含元素e，递归算法
    private boolean contains(Node node, E e) {
        if (node == null) {
            return false;
        }
        if (e.compareTo(node.e) == 0) {
            return true;
        } else if (e.compareTo(node.e) > 0) {
            return contains(node.left, e);
        } else {
            return contains(node.right, e);
        }
    }

什么是遍历操作
- 遍历操作就是把所有节点都访问一遍
- 访问的原因和业务相关
- 在线性结构下，遍历是极其容易的
- 对于遍历操作，两颗子树都要顾及

    // 二分搜索树的前序遍历
    public void preOrder(){
        preOrder(root);
    }
    // 前序遍历以node为根的二分搜索树，递归算法
    private void preOrder(Node node){
        if (node == null){
            return;
        }
        System.out.println(node.e);
        preOrder(node.left);
        preOrder(node.right);
    }

也可以这样

    // 前序遍历以node为根的二分搜索树，递归算法
    private void preOrder(Node node) {
//        if (node == null){
//            return;
//        }
        if (node != null) {
            System.out.println(node.e);
            preOrder(node.left);
            preOrder(node.right);
        }

    }

Main方法测试一下

public class Main {
    public static void main(String[] args) {
        BST<Integer> bst = new BST<>();
        int[] nums = {5, 3, 6, 8, 4, 2};
        for (int num : nums) {
            bst.add(num);
        }
        bst.preOrder();
    }
}

重写一下toString方法，方便观察树

    @Override
    public String toString() {
        StringBuilder res = new StringBuilder();
        generateBSTString(root, 0, res);
        return res.toString();
    }

    // 生成以node为根节点，深度为depth的描述二叉树的字符串
    private void generateBSTString(Node node, int depth, StringBuilder res) {
        if (node == null) {
            res.append(generateDepthString(depth) + "null\n");
            return;
        }
        res.append(generateDepthString(depth) + node.e + "\n");
        generateBSTString(node.left, depth + 1, res);
        generateBSTString(node.right, depth + 1, res);
    }

    private String generateDepthString(int depth) {
        StringBuilder res = new StringBuilder();
        for (int i = 0; i < depth; i++) {
            res.append("---");
        }
        return res.toString();
    }

五、二分搜索树的中序遍历和后序遍历

中序遍历

    // 二分搜索树的中序遍历
    public void inOrder(){
        inOrder(root);
    }
    // 中序遍历以node为根的二分搜索树，递归算法
    private void inOrder(Node node){
        if (node == null){
            return;
        }
        inOrder(node.left);
        System.out.println(node.e);
        inOrder(node.right);
    }

看结果

可以发现居然是顺序的！
特点：二分搜索树的中序遍历结果是顺序的
- 冷知识：我们之前都需要进行各种操作，才能让数据是顺序的，而这个二分搜索树，只要我们使用中序排序就是顺序的了，是不是很有意思？

后序遍历

    // 二分搜索树的后续排序
    public void postOrder(){
        postOrder(root);
    }
    // 后序遍历以node为根的二分搜索树，递归算法
    private void postOrder(Node node){
        if (node == null){
            return;
        }
        postOrder(node.left);
        postOrder(node.right);
        System.out.println(node.e);
    }

看结果

后序遍历的一个应用：
- 为二分搜索树释放内存
- JAVA来说，我们有自动的垃圾回收机制，不需要我们处理

六、二分搜索树前序遍历的非递归实现

    // 二分搜索树的非递归前序遍历
    public void preOrderNR() {
        Stack<Node> stack = new Stack<Node>();
        stack.push(root);
        while (!stack.isEmpty()) {
            Node cur = stack.pop();
            System.out.println(cur.e);

            if (cur.right != null) {
                stack.push(cur.right);
            }
            if (cur.left != null) {
                stack.push(cur.left);
            }
        }
    }

结果如下

二分搜索树遍历的非递归实现，比递归实现复杂得多
中序遍历和后序遍历的非递归实现更复杂
中序遍历和后序遍历的非递归实现，实际应用不广

七、二分搜索树的层序遍历——广度优先遍历

    // 二分搜索树的层序遍历
    public void levelOrder() {
        Queue<Node> q = new LinkedList<>();
        q.add(root);
        while (!q.isEmpty()) {
            Node cur = q.remove();
            System.out.println(cur.e);
            if (cur.left != null) {
                q.add(cur.left);
            }
            if (cur.right != null) {
                q.add(cur.right);
            }
        }
    }

结果输出

之前我们学的那种叫做深度优先遍历
广度优先遍历的意义
- 更快的找到问题的解
- 常用于算法设计中 - 最短路径

八、二分搜索树————删除元素

从最简单的开始，删除二分搜索树的最小值和最大值

   // 寻找二分搜索树的最小元素
    public E minimum() {
        if (size == 0) {
            throw new IllegalArgumentException("BST is empty!");
        }
        return minimum(root).e;
    }

    // 返回以node为根的二分搜索树的最小值所在的节点
    private Node minimum(Node node) {
        if (node.left == null) {
            return node;
        }
        return minimum(node.left);
    }

    // 寻找二分搜索树的最大元素
    public E maximum() {
        if (size == 0) {
            throw new IllegalArgumentException("BST is empty!");
        }
        return maximum(root).e;
    }

    // 返回以node为根的二分搜索树的最大值所在的节点
    private Node maximum(Node node) {
        if (node.right == null) {
            return node;
        }
        return maximum(node.right);
    }

    // 从二分搜索树中删除最小值所在节点，返回最小值
    public E removeMin() {
        E ret = minimum();
        root = removeMin(root);
        return ret;
    }

    // 删除掉以node为根的二分搜索树中的最小节点
    // 返回删除节点后新的二分搜索树的根
    private Node removeMin(Node node) {
        if (node.left == null) {
            Node rightNode = node.right;
            node.right = null;
            size -- ;
            return rightNode;
        }
        node.left = removeMin(node.left);
        return node;
    }

    // 从二分搜索树中删除最小值所在节点，返回最大值
    public E removeMax() {
        E ret = maximum();
        root = removeMax(root);
        return ret;
    }

    // 删除掉以node为根的二分搜索树中的最大节点
    // 返回删除节点后新的二分搜索树的根
    private Node removeMax(Node node) {
        if (node.right == null) {
            Node leftNode = node.left;
            node.left = null;
            size -- ;
            return leftNode;
        }
        node.right = removeMax(node.right);
        return node;
    }

测试代码

点击查看完整内容

package bst;

import java.util.ArrayList;
import java.util.Random;

public class Main {
    public static void main(String[] args) {
        BST<Integer> bst = new BST<>();
        BST<Integer> bst2 = new BST<>();
        Random random = new Random();
        int n = 1000;
        for (int i = 0; i < n; i++) {
            bst.add(random.nextInt(10000));
            bst2.add(random.nextInt(10000));
        }
        ArrayList<Integer> nums1 = new ArrayList<>();
        ArrayList<Integer> nums2 = new ArrayList<>();

        while (!bst.isEmpty()) {
            nums1.add(bst.removeMin());
        }
        while (!bst2.isEmpty()) {
            nums2.add(bst2.removeMax());
        }
        System.out.println(nums1);

        for (int i = 1; i < nums1.size(); i++) {
            if (nums1.get(i - 1) > nums1.get(i)) {
                throw new IllegalArgumentException("Error");
            }
        }
        System.out.println("成功！");
        System.out.println(nums2);
        for (int i = 1; i < nums1.size(); i++) {
            if (nums2.get(i - 1) < nums2.get(i)) {
                throw new IllegalArgumentException("Error");
            }
        }
        System.out.println("成功！");
    }
}

结果输出

九、删除二分搜索树的任意节点

    // 从二分搜索树中删除元素为e的节点
    public void remove(E e) {
        root = remove(root, e);
    }

    //删除以node为根的二分搜索树中值为e的节点，递归算法
    // 返回删除节点后新的二分搜索树的根
    private Node remove(Node node, E e) {
        if (node == null) {
            return null;
        }
        if (e.compareTo(node.e) < 0) {
            node.left = remove(node.left, e);
            return node;
        } else if (e.compareTo(node.e) > 0) {
            node.right = remove(node.right, removeMin());
            return node;
        } else {
            // e == node.e
            // 待删除节点左子树为空的情况
            if (node.left == null) {
                Node rightNode = node.right;
                node.right = null;
                size++;
                return rightNode;
            }
            // 待删除节点右子树为空的情况
            if (node.right == null) {
                Node leftNode = node.left;
                node.left = null;
                size--;
                return leftNode;
            }
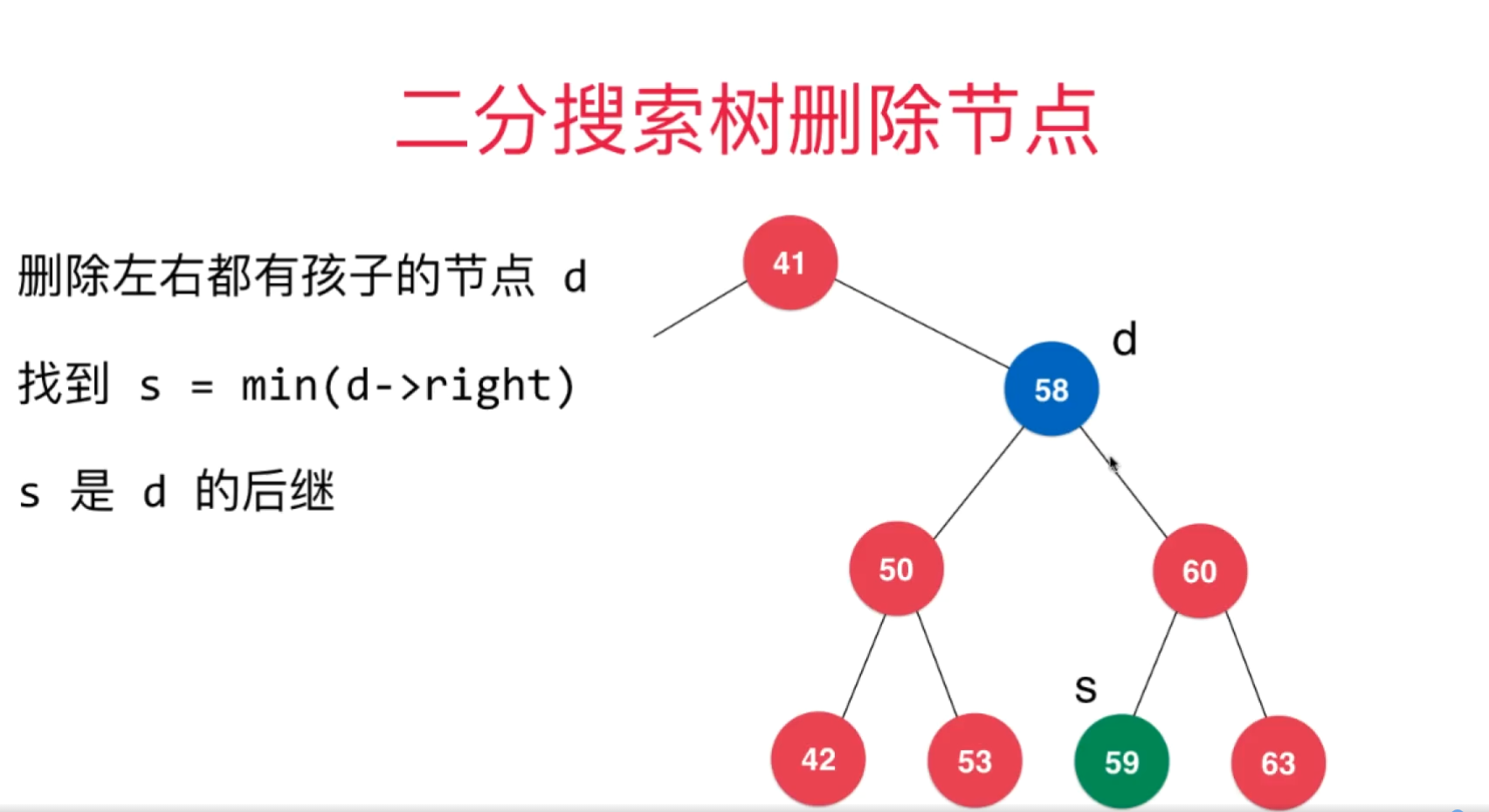
            // 待删除节点左右子树均不为空的情况
            // 找到比待删除节点大的最小节点，即待删除节点右子树的最小节点
            // 用这个节点顶替待删除节点的位置
            Node successor = minimum(node.right);
            successor.right = removeMin(node.right);
            successor.left = node.left;

            node.left = node.right = null;
            return successor;
        }
    }

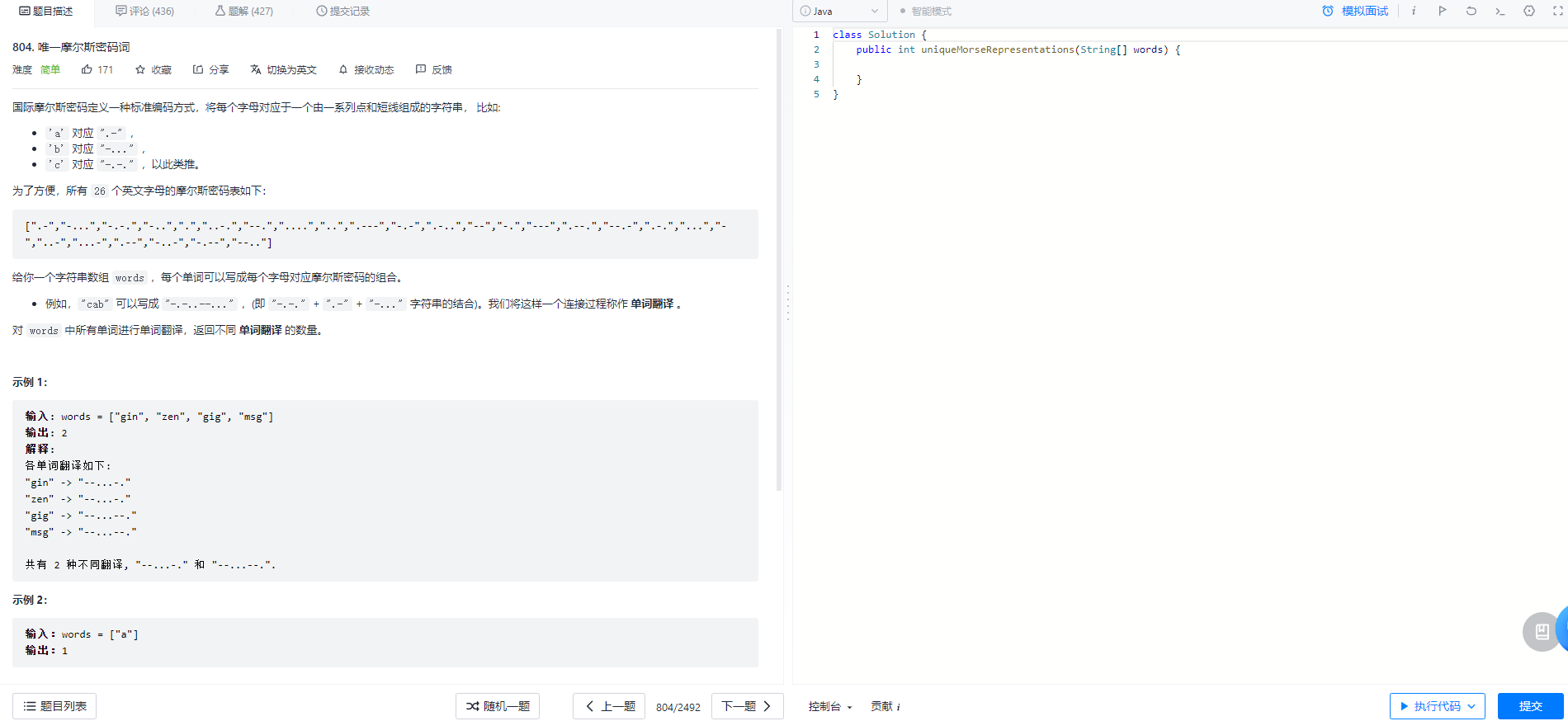
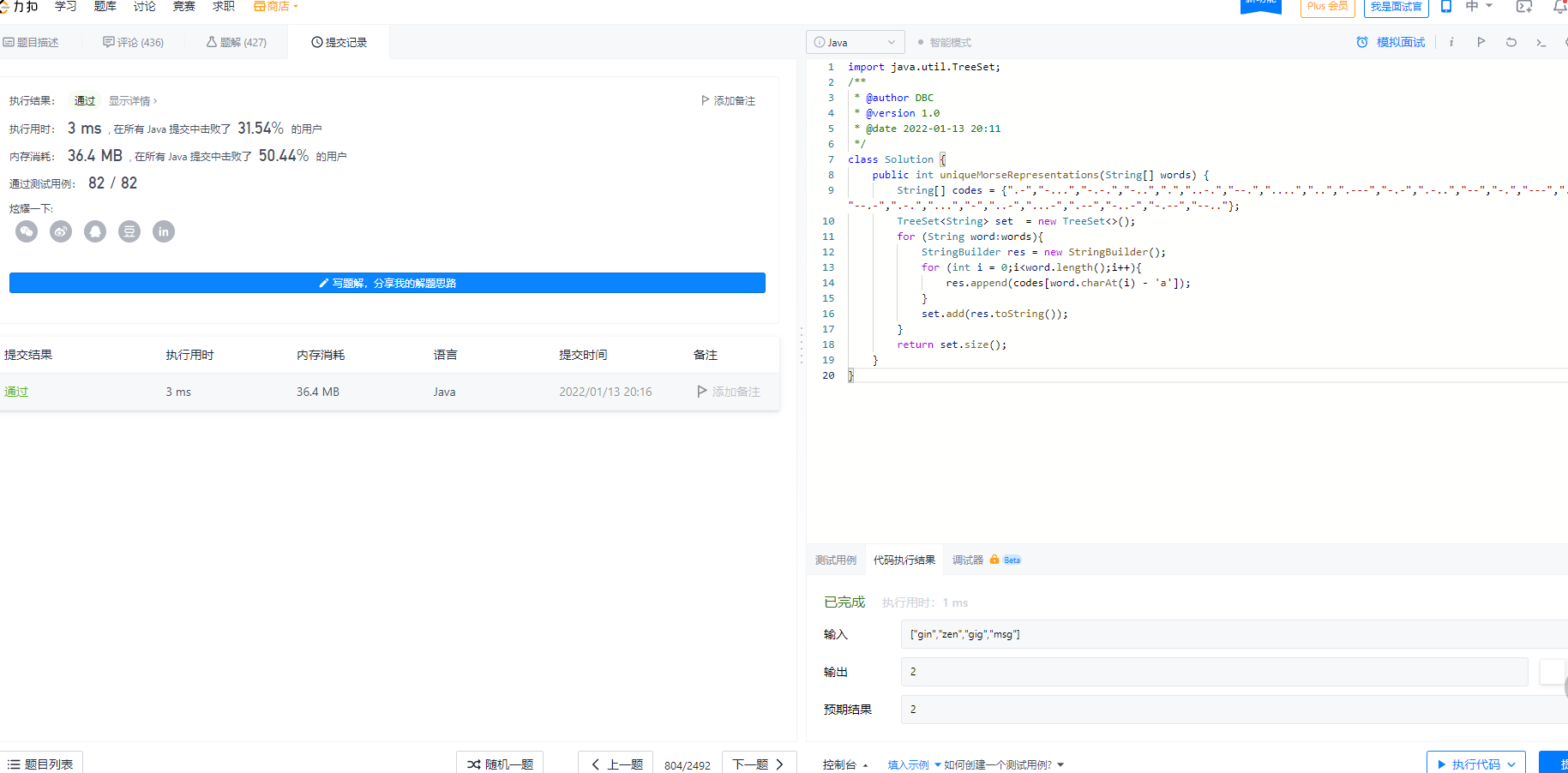
十、力扣题目 804

package Solution7;
import java.util.TreeSet;
/**
 * @author DBC
 * @version 1.0
 * @date 2022-01-13 20:11
 */
class Solution {
    public int uniqueMorseRepresentations(String[] words) {
        String[] codes = {".-","-...","-.-.","-..",".","..-.","--.","....","..",".---","-.-",".-..","--","-.","---",".--.","--.-",".-.","...","-","..-","...-",".--","-..-","-.--","--.."};
        TreeSet<String> set  = new TreeSet<>();
        for (String word:words){
            StringBuilder res = new StringBuilder();
            for (int i = 0;i<word.length();i++){
                res.append(codes[word.charAt(i) - 'a']);
            }
            set.add(res.toString());
        }
        return set.size();
    }
}

- 有序集合中的元素具有顺序性通常基于搜索树的实现
- 无序集合中的元素没有顺序性通常基于哈希表的实现
多重集合
- 集合中的元素可以重复

十一、映射

public interface Map<K, V> {
    void add(K key, V value);

    V remove(K key);

    boolean contains(K key);

    V get(K key);

    void set(K key, V newValue);

    int getSize();

    boolean isEmpty();

}

本文作者为DBC，转载请注明。

算法