二分查找法

一、基本概念

对于有序数列，才能使用二分查找法

• 时间复杂度：O（logn）级别
• 我们没有把排序时间算进去
  • 排序叫做二分查找法的前置条件
  • 如果计算排序时间：O（nlogn）
  • 应用：多次查找

• 二分查找法的思想在1946年提出
• 第一个没有bug的二分查找法在1962年才出现
• mid = ( l + r  ) / 2 可能整型溢出
• mid = l + ( r - l ) / 2

二、二分查找法简单实现

public class BinarySearch {
    private BinarySearch() {
    }

    public static <E extends Comparable<E>> int search(E[] data, E target) {
        return search(data, 0, data.length - 1, target);
    }

    private static <E extends Comparable<E>> int search(E[] data, int l, int r, E target) {
        if (l > r) {
            return -1;
        }
        int mid = l + (r - l) / 2;
        if (data[mid].compareTo(target) == 0) {
            return mid;
        }
        if (data[mid].compareTo(target) < 0) {
            return search(data, mid + 1, r, target);
        }
        return search(data, l, mid - 1, target);
    }
}

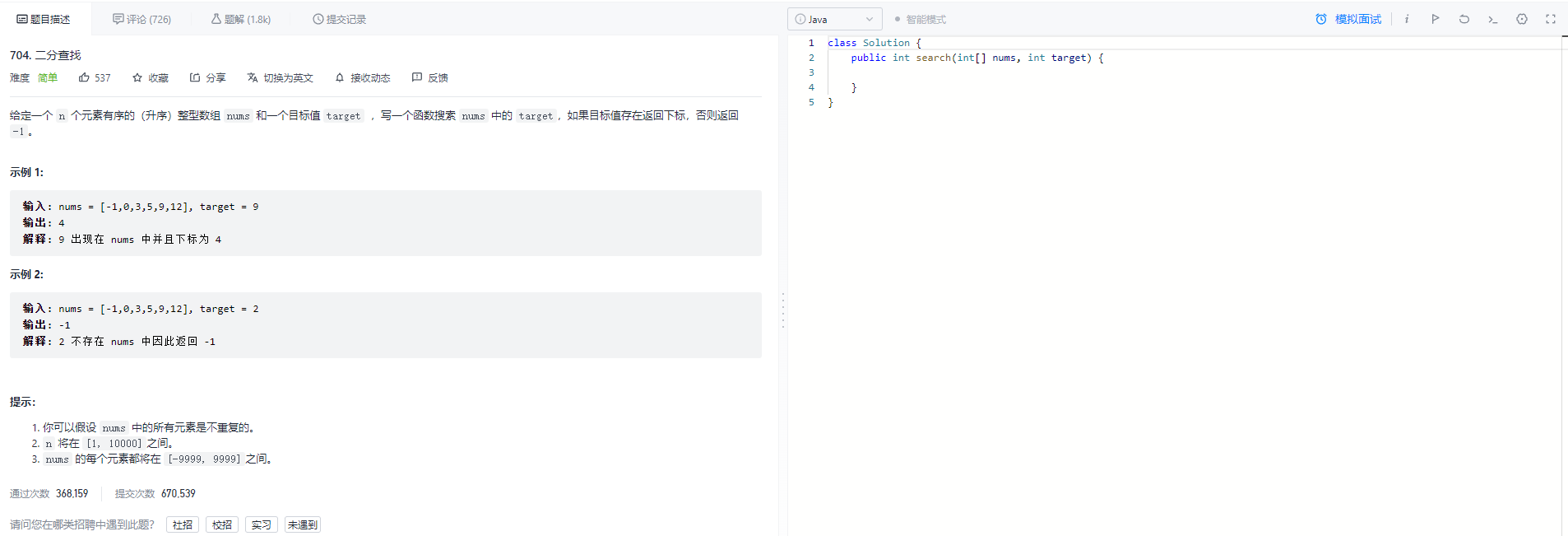
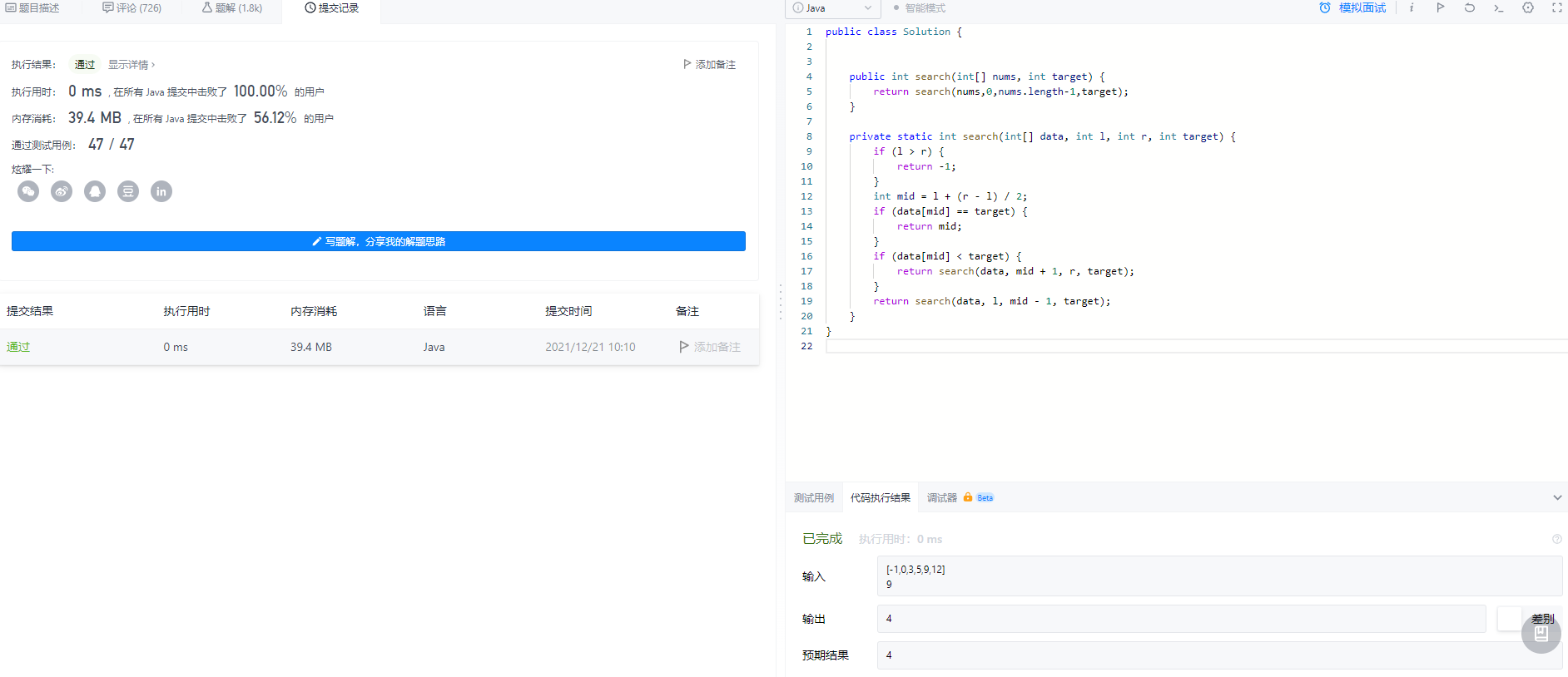
来看一个力扣题目——704. 二分查找

public class Solution {


    public int search(int[] nums, int target) {
        return search(nums,0,nums.length-1,target);
    }
    
    private static int search(int[] data, int l, int r, int target) {
        if (l > r) {
            return -1;
        }
        int mid = l + (r - l) / 2;
        if (data[mid] == target) {
            return mid;
        }
        if (data[mid] < target) {
            return search(data, mid + 1, r, target);
        }
        return search(data, l, mid - 1, target);
    }
}

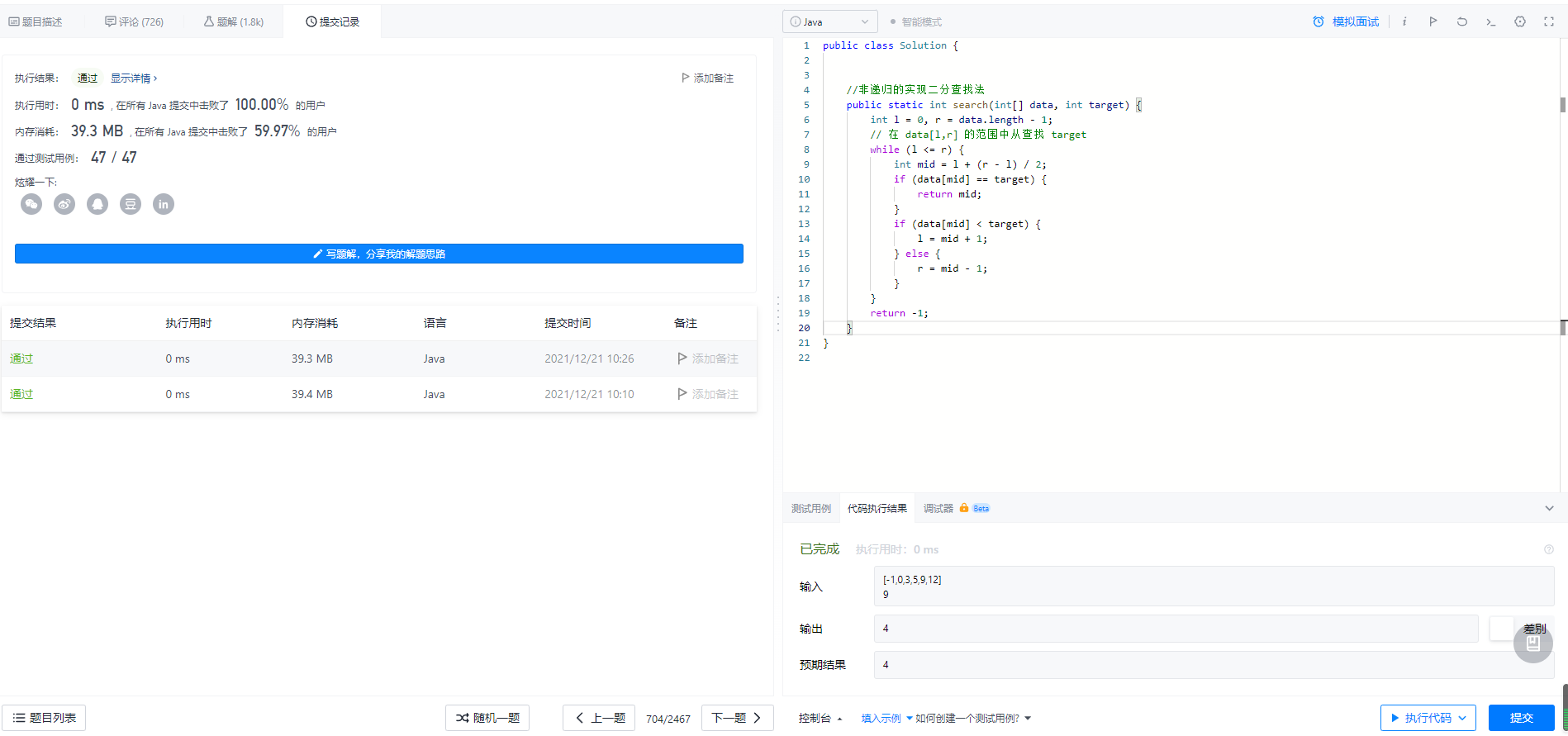
三、非递归的实现二分查找法

    //非递归的实现二分查找法
    public static <E extends Comparable<E>> int search(E[] data, E target) {
        int l = 0, r = data.length - 1;
        // 在 data[l,r] 的范围中从查找 target
        while (l <= r) {
            int mid = l + (r - l) / 2;
            if (data[mid].compareTo(target) == 0) {
                return mid;
            }
            if (data[mid].compareTo(target) < 0) {
                l = mid + 1;
            } else {
                r = mid - 1;
            }
        }
        return -1;
    }

将这个非递归的方法放到力扣题目中，依然是可以实现的

    //非递归的实现二分查找法
    public static int search(int[] data, int target) {
        int l = 0, r = data.length - 1;
        // 在 data[l,r] 的范围中从查找 target
        while (l <= r) {
            int mid = l + (r - l) / 2;
            if (data[mid] == target) {
                return mid;
            }
            if (data[mid] < target) {
                l = mid + 1;
            } else {
                r = mid - 1;
            }
        }
        return -1;
    }

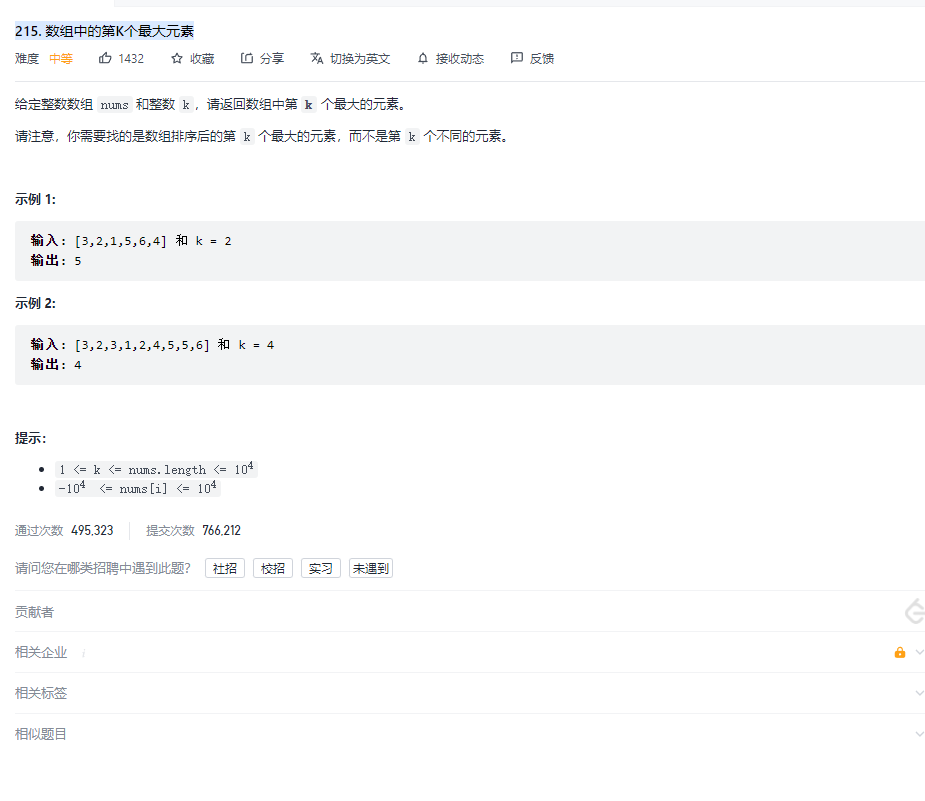
四、我们以非递归的实现Select K 算法

依然是我们的力扣 215 题

在这一小节，我们主要修改之前的递归的selectK函数：

    private int selectK(int[] arr, int l, int r, int k, Random rnd) {
        int p = partition(arr, l, r, rnd);
        if (k == p) {
            return arr[p];
        }
        if (k < p) {
            return selectK(arr, l, p - 1, k, rnd);
        }
        return selectK(arr, p + 1, r, k, rnd);

    }

现在，因为我们的算法是非递归了，所以，已经不需要在函数中传i和r两个参数了，因此，函数签名发生了改变，变成了这个样子：

    private int selectK(int[] arr,  int k, Random rnd) {
    }

• 只是扔掉了原先的 l ， r 两个参数而已
• 我们在这个基础上，我们来看具体逻辑
  • 其实，和上一小节我们介绍的二分搜索树的非递归算法非常像，我们将在一个循环中，不断变更我们的搜索范围，我们的循环将维持一个循环不变量：我们要在arr[l,r]的范围里寻找第k小的数字。
  • 因此，初始，我们的 l 值 为0；r 值为arr.lenggth() - 1 ，表示在初始，我们要在整个数组范围里寻找答案。
  • 我们的循环继续条件是 while（l  <=  r），因为只要 l < r ，意味着我们的搜索范围里还有解，就要继续循环的过程。
  • 在循环里面，如果没有找到解，那么，如果 k < p，我们就要继续在p的左边寻找。相应的，我们需要改变 r 的值，让 r = p - l；
  • 如果 k > p ,我们就要继续在 p 的右边寻找。相应的，我们需要改变 l 的值。让 l =  p + l

具体代码

    private int selectK(int[] arr, int k, Random rnd) {
        int l = 0, r = arr.length - 1;
        while (l <= r) {
            int p = partition(arr, l, r, rnd);
            if (k == p) {
                return arr[p];
            }
            if (k < p) {
                r = p - 1;
            } else {
                l = p + 1;
            }
        }
        throw new RuntimeException("No Solution");

    }

完整代码

package solution4;

import List.Array;

import java.util.Arrays;
import java.util.Random;

class Solution {
    public int findKthLargest(int[] nums, int k) {

        Random rnd = new Random();

        return selectK(nums,nums.length - k,rnd);
    }

    private int selectK(int[] arr, int k, Random rnd) {
        int l = 0, r = arr.length - 1;
        while (l <= r) {
            int p = partition(arr, l, r, rnd);
            if (k == p) {
                return arr[p];
            }
            if (k < p) {
                r = p - 1;
            } else {
                l = p + 1;
            }
        }
        throw new RuntimeException("No Solution");

    }

    private int partition(int[] arr, int l, int r, Random rnd) {
        // 生成[l,r] 之间的随机索引
        int p = l + rnd.nextInt(r - l + 1);
        swap(arr, l, p);

        //arr[l+1...i-1] <= v; arr[j+1...r] >= v
        int i = l + 1, j = r;
        while (true) {
            while (i <= j && arr[i] < arr[l]) {
                i++;
            }
            while (j >= i && arr[j] > arr[l]) {
                j--;
            }
            if (i >= j) {
                break;
            }
            swap(arr, i, j);
            i++;
            j--;
        }
        swap(arr, l, j);
        return j;
    }

    private void swap(int[] arr, int i, int j) {
        int t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;
    }
}

力扣测试

五、换个定义实现二分查找法

    //非递归的实现二分查找法
    public static int search(int[] data, int target) {
        int l = 0, r = data.length;
        // 在 data[l,r] 的范围中从查找 target
        while (l < r) {
            int mid = l + (r - l) / 2;
            if (data[mid] == target) {
                return mid;
            }
            if (data[mid] < target) {
                l = mid + 1; // 继续在 data[mid + 1，r] 范围里寻找解
            } else {
                r = mid; // 继续在 data[l,mid] 范围里寻找解
            }
        }
        return -1;
    }

力扣测试——依然可以实现

六、利用二分查找法来解决一个问题 —— 大于target 的最小值索引

    // > target 的最小值索引
    public static <E extends Comparable<E>> int upper(E[] data, E target) {
        int l = 0, r = data.length;

        // 在data[l,r] 中寻找解
        while (l < r) {
            int mid = l + (r - l ) / 2;
            if (data[mid].compareTo(target)<=0){
                l = mid +1;
            }else {
                r = mid;
            }

        }
        return l;
    }

    public static void main(String[] args) {
        Integer[] arr = {1,2,3,4,5,6,6,7,8};
        for (int i = 0; i<= 9;i++){
            System.out.print(BinarySearch.upper(arr,i)+" ");
        }
    }

七、ceil例子，具体说明如下

• • • 查找 5 如果数组中存在元素，则返回最大索引   例子中返回  5
    • 查找 6 如果数组中不存在元素，返回 upper   例子中返回  6
    • 例子： 1 , 1 , 3 , 3 , 5 , 5 , 7 , 7

具体代码

    // > target , 返回最小值索引
    // == target , 返回最大索引
    public static <E extends Comparable<E>> int ceil(E[] data, E target) {
        int u = upper(data, target);
        if (u - 1 >= 0 && data[u - 1].compareTo(target) == 0) {
            return u - 1;
        }
        return u;
    }

    public static void main(String[] args) {
        Integer[] arr = {1, 2, 2, 4, 5, 6, 6, 7, 8};
        for (int i = 0; i <= 9; i++) {
            System.out.print(BinarySearch.ceil(arr, i) + " ");
        }
    }

八、二分查找法的变种——lower_ceil（>=target 的最小索引）

• 查找5 如果数组中存在元素，返回最小索引
• 查找6 如果数组中不存在元素，返回upper

具体代码

    public static <E extends Comparable<E>> int lower_ceil(E[] data, E target) {
        int l = 0, r = data.length;

        // 在data[l,r] 中寻找解
        while (l < r) {
            int mid = l + (r - l) / 2;
            // 在 upper中，这里是 data[mid].compareTo(target) <= 0
            // 但是，对于lower_ceil 来说，在 data[mid] == target的时候，有可能是解
            // 所以在等于的情况下，不能排除掉 data[mid]的值。在等于的情况下，应该归入下面的
            // 也就是，data[mid] == target 的时候可能是解，也可能有更小的解在左边

            if (data[mid].compareTo(target) < 0) {
                l = mid + 1;
            } else {
                r = mid;
            }

        }
        return l;
    }

九、查找小于 target 的最大值 —— lower

• • 搜索范围 arr[l,r] l = -1
  • 例子： 23 , 56 , 65 , 69 , 72 , 89 , 96 , 99
    • 假设找 target = 85 ，那么应该找到的是72

具体代码

    // < target 的最大值索引
    public static <E extends Comparable<E>> int lower(E[] data, E target) {
        int l = -1, r = data.length - 1;
        // 在 data[l，r] 中寻找解
        while (l < r) {
            int mid = l + (r - l + 1) / 2;
            if (data[mid].compareTo(target) < 0) {
                l = mid;
            } else {
                r = mid - 1;
            }
        }
        return l;
    }

• • • 这里有一个重要的BUG，一定要注意喔 这一行代码 int mid = l + (r - l + 1) / 2;
    • 之前我们的代码一直都是 int mid = l + (r - l) / 2; ，这个能看出来区别吗？
      • 当我们的l、r相邻的时候，而target又在这里，就会触发无限循环的BUG，很多教程会让我们在这里进行if判断一下，非常的不优雅，这里我们使用慕课算法名师——波波老师的优化，看起来就非常的优雅。具体原因感兴趣的可以自己敲代码进入然后看看效果。

测试结果如下

    public static void main(String[] args) {
        Integer[] arr = {1, 1, 3, 3, 5, 5};
        for (int i = 0; i <= 6; i++) {
            System.out.print(BinarySearch.lower(arr, i) + " ");
        }
    }

十、我们再来看两个小例子：lower_floor 、 upper_floor

具体代码

lower_floor

    // < target 返回最大值索引
    // == target 返回最小索引
    public static <E extends Comparable<E>> int lower_floor(E[] data, E target) {
        int l = lower(data, target);
        // 注意，因为我们要访问 data[l +1]，所以，我们要先确保 l + 1 不越界
        // 即 l + 1 < data.length
        if (l + 1 < data.length && data[l + 1].compareTo(target) == 0) {
            return l + 1;
        }
        return l;
    }

upper_floor

    // <= target 最大索引
    public static <E extends Comparable<E>> int upper_floor(E[] data, E target) {
        int l = -1, r = data.length - 1;
        // 在 data[l，r] 中寻找解
        while (l < r) {
            int mid = l + (r - l + 1) / 2;
            //为什么 upper_floor 同样需要使用上取整的方式来计算 mid？

            // 在 lower 中，这里是 data[mid].compareTo(target) < 0
            // 但是，对于 upper_floor来说，在 data[mid]  == target 的时候，有可能是解
            // 所以在等于的情况下，不能排除掉 data[mid] 的值，我们的搜索空间变化，通用是l = mid
            if (data[mid].compareTo(target) <= 0) {
                l = mid;
            } else {
                r = mid - 1;
            }
        }
        return l;
    }

结果输出

    public static void main(String[] args) {
        Integer[] arr = {1, 1, 3, 3, 5, 5};
        System.out.print("lower_floor :");
        for (int i = 0; i <= 6; i++) {
            System.out.print(BinarySearch.lower_floor(arr, i) + " ");
        }
        System.out.println();
        System.out.print("upper_floor :");
        for (int i = 0; i <= 6; i++) {
            System.out.print(BinarySearch.upper_floor(arr, i) + " ");
        }
    }

十一、很多时候，和二分查找法相关的算法问题，不是在数组中寻找值，而是使用二分查找法，搜索问题的解

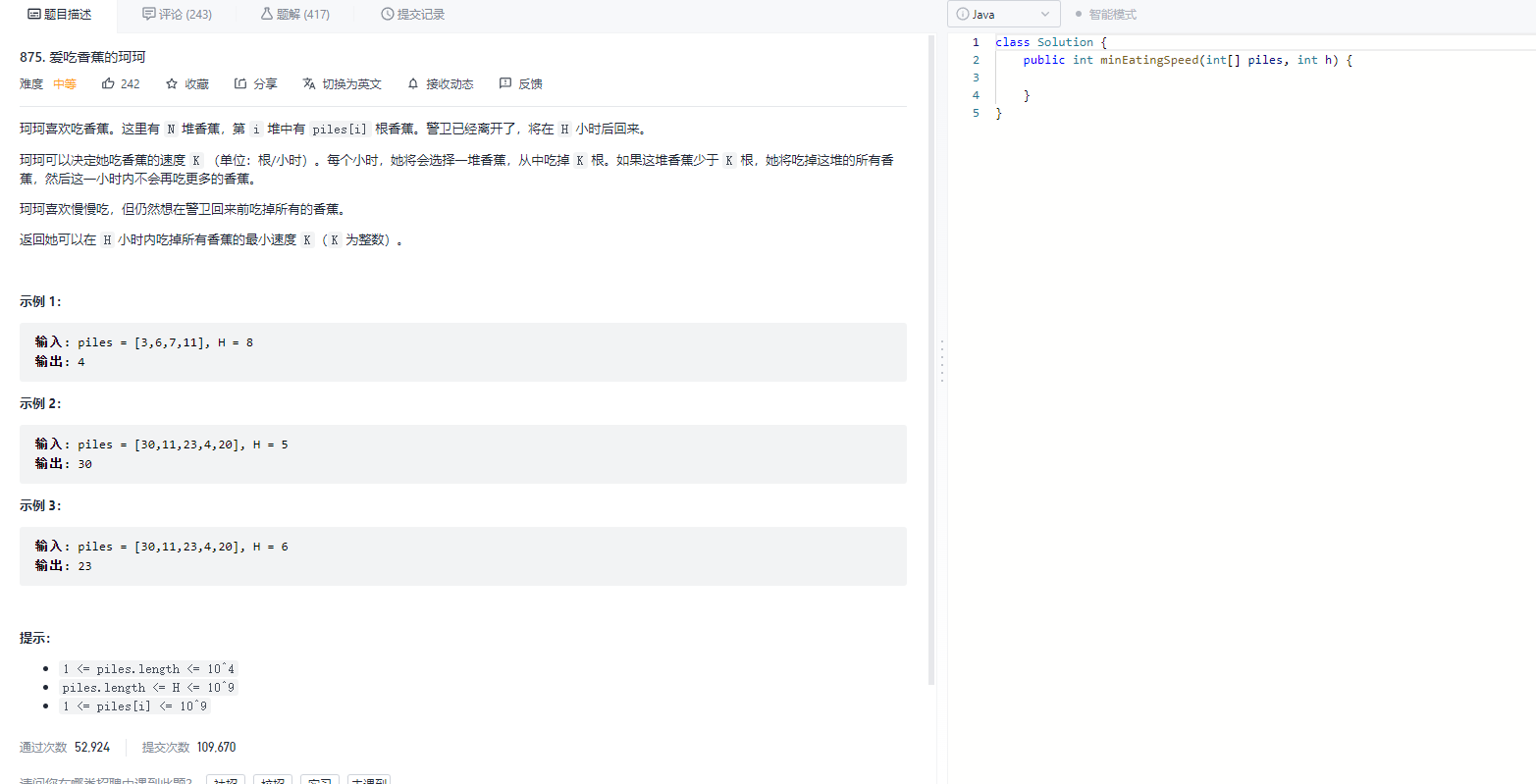
我们来看力扣875题

具体代码

class Solution {
    public int minEatingSpeed(int[] piles, int h) {
        int l = 1, r = Arrays.stream(piles).max().getAsInt();
        while (l < r) {
            int mid = l + (r - l) / 2;
            if (eatingTime(piles, mid) <= h) {
                r = mid;
            } else {
                l = mid + 1;
            }
        }
        return l;
    }

    private int eatingTime(int[] piles, int k) {
        int res = 0;
        for (int pile : piles) {
            res += pile / k + (pile % k > 0 ? 1 : 0);
        }
        return res;
    }
}

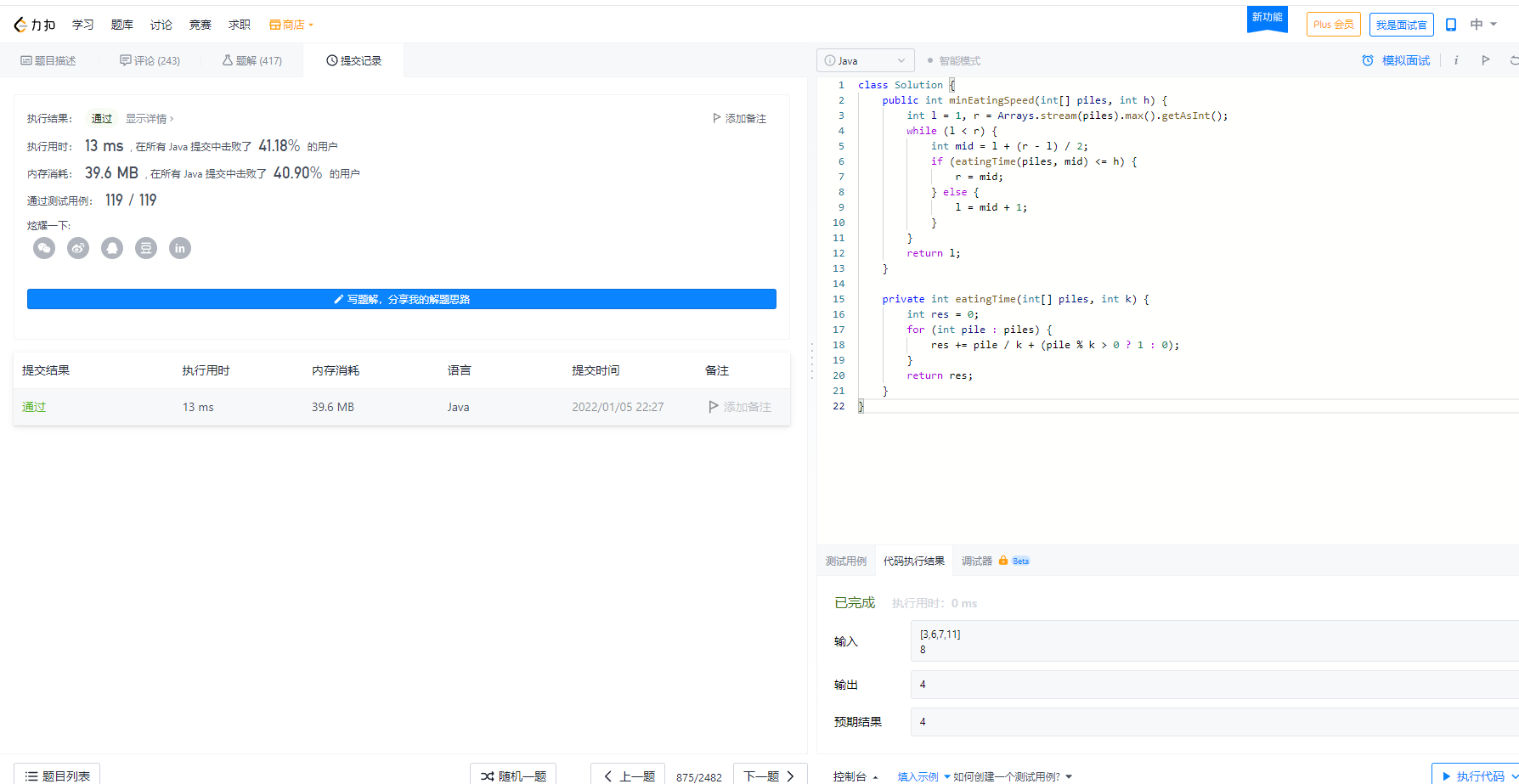
输出结果

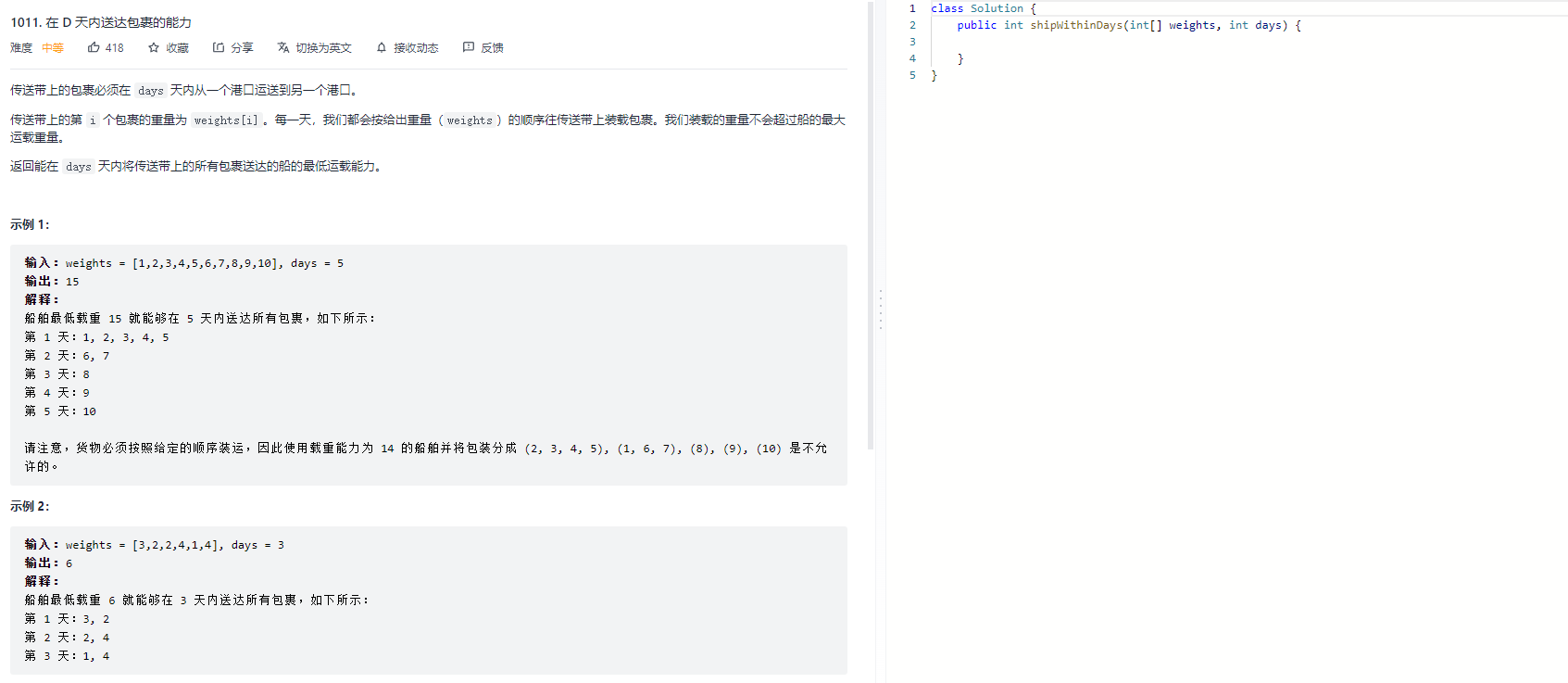
再来看一题：力扣1011

class Solution {
    public int shipWithinDays(int[] weights, int D) {
        int l = Arrays.stream(weights).max().getAsInt();
        int r = Arrays.stream(weights).sum();
        while (l < r) {
            int mid = l + (r - l) / 2;
            // 如果传送带运载能力是mid，运完货物需要的天数小于等于D
            // 那么mid就是一个可能的解，但是，我们还要找，看有没有更小的解
            // 所以，调整右边界，r= mid。
            // 注意，mid要包含在搜索范围里,因为mid是问题的解
            if (days(weights, mid) <= D) {
                r = mid;

            }
            // 否则的话，运完货物需要的天数大于D
            // 我们就需要加大传送带的运载能力，以在更短的时间里运送所有货物
            // 因此，我们调整左边界，l= mid + 1。
            // 注意，mid 不再包含在搜索空间中，因为此时，mid不是问题的解
            else {
                l = mid + 1;
            }
            // 在决定好搜索空间的调整方式后，我们可以试验一下，如果l，r相邻，是否会出现死循环?
            // 在这个例子中，因为下取整以后，在l和r相临时，mid为1。而对1的更新，是 mid + 1
            // 所以保证了在这种情况下，搜索空间会继续缩小，不会产生死循环
            // 因此，使用下取整来计算mid是可以的
        }
        return l;

    }

    private int days(int[] weights, int k) {
        // cur 为当前传送带的载重;res为最终的返回结果
        int cur = 0, res = 0;
        // 遍历weights 中的每一个元素
        for (int weight : weights) {
            // 如果当前的重量加上当前的货物没有超过k，
            // 把当前货物重量加在 cur 上
            if (cur + weight <= k) {
                cur += weight;
            }
            // 否则的话，相当于从当前的货物开始，我们需要新的一天运输
            // res ++，同时，cur更新为当前的重量
            else {
                res++;
                cur = weight;
            }
        }
        // 最后还要做一次res *+，因为在这里cur肯定不为零，还记录着最后一天需要运送的货物重量
        // 最后一天，要加到 res中，所以res ++
        res++;
        return res;
    }

}