快速排序法——传说中的无敌算法！影响了一个世纪！超级大汇总—

一、快速排序法的原理

温馨提示

看上面的图，快速排序法就是我们找到这个4的位置，而4之前的值都会比4小，之后的值都会比4大，所以说，我们怎么找到这个4，就是排序算法的关键了，当我们找到后，在4左右的两边数组，同样原理，递归下去，最终完成排序！

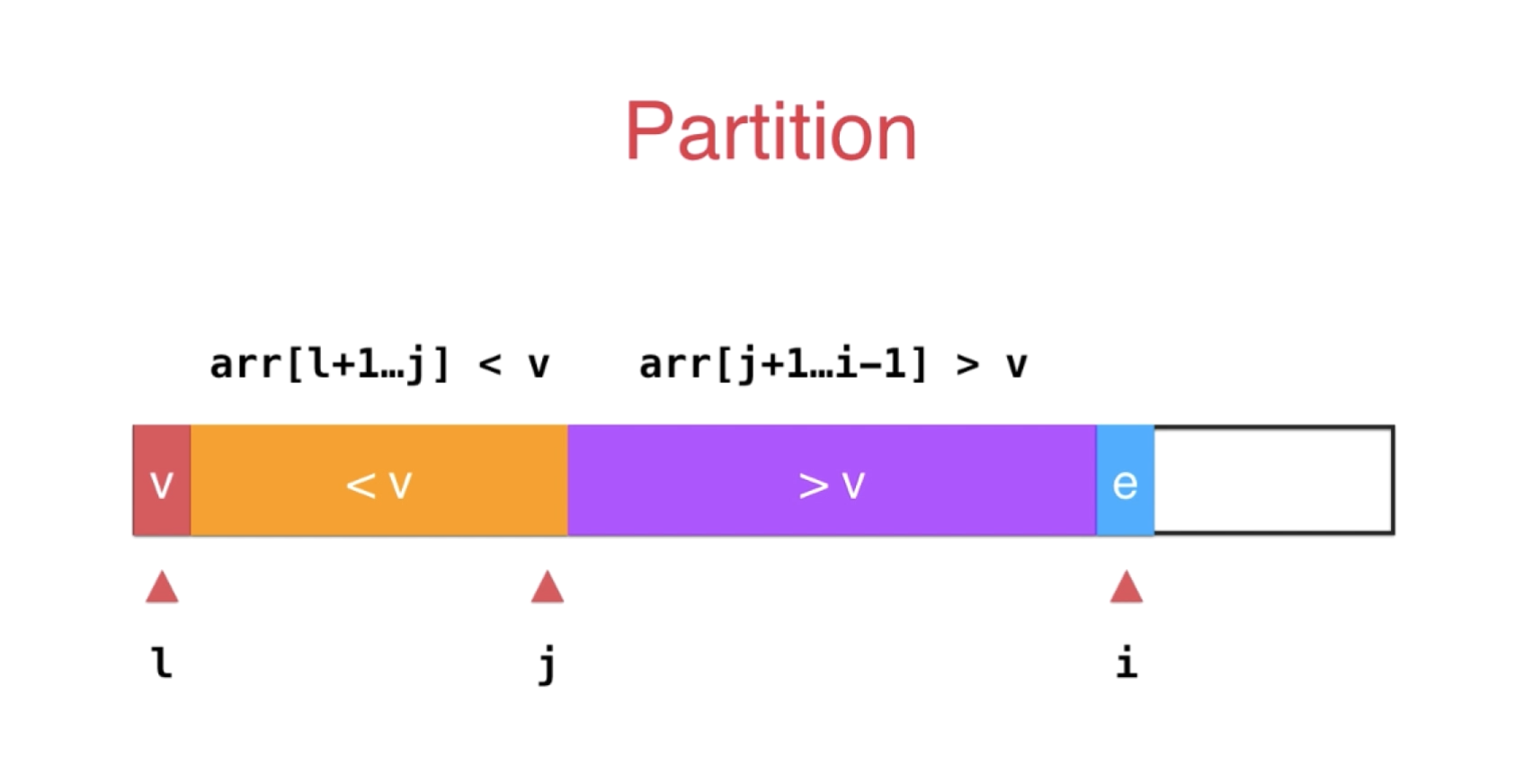
二、Partition

我们通过partition这个函数，就能够实现我们上面的需求，那么我们的partition函数该如何写呢，看下面的图，相信很容易理解，我们慢慢深入看它

温馨提示

这里要注意，经过partition之后，数组并没有完成排序，仅仅是将数组分成了由v来分割的两个数组！

第一版快速排序法

package quicksort;

import List.Array;
import MergeSort.ArrayGenerator;
import MergeSort.SortingHelper;

import java.util.Arrays;

public class QuickSort {
    private QuickSort() {
    }

    public static <E extends Comparable<E>> void sort(E[] arr) {
        sort(arr, 0, arr.length - 1);
    }

    private static <E extends Comparable<E>> void sort(E[] arr, int l, int r) {
        if (l >= r) {
            return;
        }
        int p = partition(arr, l, r);
        sort(arr, l, p - 1);
        sort(arr, p + 1, r);
    }

    private static <E extends Comparable<E>> int partition(E[] arr, int l, int r) {
        // arr[l+1...j] < v; arr[j+1...i] >= v
        int j = l;
        for (int i = l + 1; i <= r; i++) {
            if (arr[i].compareTo(arr[l]) < 0) {
                j++;
                swap(arr, i, j);
            }
        }
        swap(arr, l, j);
        return j;
    }


    /**
     * 简单的数组元素交换
     *
     * @param arr
     * @param i
     * @param j
     * @param <E>
     */
    private static <E> void swap(E[] arr, int i, int j) {
        E t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;

    }

    public static void main(String[] args) {
        int n = 10000000;
        Integer[] arr = ArrayGenerator.generateRandomArray(n,n);
        Integer[] arr2 = Arrays.copyOf(arr,arr.length);

        SortingHelper.sortTest("MergeSort",arr);
        SortingHelper.sortTest("QuickSort",arr2);
    }
}

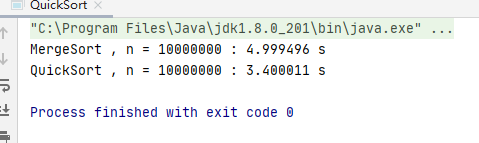
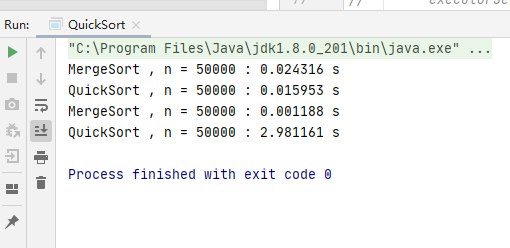
代码运行情况

温馨提示

我们可以看到在1000万长度下，快速排序法比归并排序快一些哈~ [aru_13]

三、第一版快速排序用法的问题

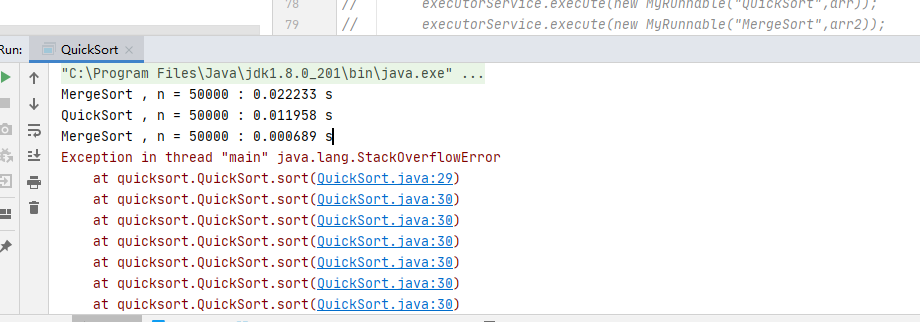
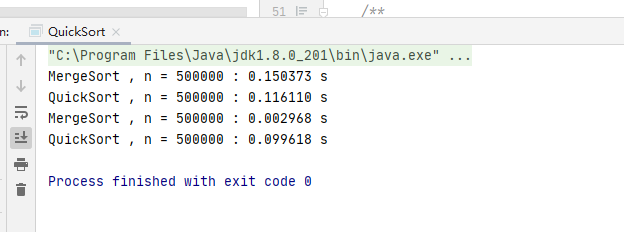
之前我们测试的是随机的数组，现在我们来测试一下完全有序的数组，看看会怎么样

温馨提示

可以看到，这时候我们的快速排序法居然提示栈溢出了，我们可以尝试一下提高一些

这时候不报错啦，但是我们也可以看到，时间居然高了那么多？

我们来看看它内部做了什么

温馨提示

可以看到，这种情况下，我们这时候的排序算法时间复杂度是O（n^2）级别的！所以就会很慢啦！ [aru_42]
让我来用大白话来说明这是什么原因：因为我们第一版快速排序算法，每次都是以第一个值来作为标定点，这时候又因为这个标定点永远都是最小的，这样一来，标定点左边永远都是没有值的，这是一种非常极端不友好的情况，因为我们是递归操作，那么我们的递归深度就会非常的深！再通俗一点就是之前我们理想情况下都能一分为二，这样的深度就会太深！

解决办法

我们的标定点不是一直使用最左边了，变成随机选一个标定点，然后把它和最左边的进行互换，这样就可以解决了！ [aru_43]

    private static <E extends Comparable<E>> int partition(E[] arr, int l, int r) {
        // 生成[l,r] 之间的随机索引
        int p = l + (new Random()).nextInt(r - l + 1);
        swap(arr, l, p);
        // arr[l+1...j] < v; arr[j+1...i] >= v
        int j = l;
        for (int i = l + 1; i <= r; i++) {
            if (arr[i].compareTo(arr[l]) < 0) {
                j++;
                swap(arr, i, j);
            }
        }
        swap(arr, l, j);
        return j;
    }

关键代码

        // 生成[l,r] 之间的随机索引
        int p = l + (new Random()).nextInt(r - l + 1);
        swap(arr, l, p);

结果输出

温馨提示

可以看到，我们的快排就已经进行了小优化了，我们发现，好像为什么对抗不了归并排序法呢？这里还可以有一个优化的地方，int p = l + (new Random()).nextInt(r - l + 1);，我们每一次都搞一次new，这样也会有一些性能消耗！
有同学可能会想这个问题，我们为什么要随机一个呢？我们不可以每一次都取最中间的那个数吗？这样的深度不会更加浅吗？
解答：因为你每一次都取最中间的值，在完全有序的情况下，确实会优化得不错，但是会存在一个问题，那就是会出现一种极端的情况，那就是你每一次取的中间数都是数组中最小的那个，这样一来，深度又上去了。因为你不可以否定，你如果使用这个算法，那么我们一定可以人为的弄出一个数组让你的算法报废！[aru_22]
有同学开始杠了！那你随机也有可能会一直随机到最小的呀！
学过概率学的小伙伴应该很能理解，这种指数级别的概率，虽然有可能会发生，但已经是近乎不可能发生了，而且你是不可以人为的创造一个数组来报废我的算法！[aru_12]

我们优化一下

完全代码

点击查看完整内容

package quicksort;

import LinearSearch.ThreadDemo4;
import List.Array;
import MergeSort.ArrayGenerator;
import MergeSort.SortingHelper;

import java.util.Arrays;
import java.util.Random;
import java.util.concurrent.*;

public class QuickSort {

    private QuickSort() {
    }

    public static <E extends Comparable<E>> void sort(E[] arr) {
        Random rnd = new Random();
        sort(arr, 0, arr.length - 1, rnd);
    }

    private static <E extends Comparable<E>> void sort(E[] arr, int l, int r, Random rnd) {
        if (l >= r) {
            return;
        }
        int p = partition(arr, l, r, rnd);
        sort(arr, l, p - 1, rnd);
        sort(arr, p + 1, r, rnd);
    }

    private static <E extends Comparable<E>> int partition(E[] arr, int l, int r, Random rnd) {
        // 生成[l,r] 之间的随机索引
        int p = l + rnd.nextInt(r - l + 1);
        swap(arr, l, p);
        // arr[l+1...j] < v; arr[j+1...i] >= v
        int j = l;
        for (int i = l + 1; i <= r; i++) {
            if (arr[i].compareTo(arr[l]) < 0) {
                j++;
                swap(arr, i, j);
            }
        }
        swap(arr, l, j);
        return j;
    }


    /**
     * 简单的数组元素交换
     *
     * @param arr
     * @param i
     * @param j
     * @param <E>
     */
    private static <E> void swap(E[] arr, int i, int j) {
        E t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;

    }

    public static void main(String[] args) {
        int n = 500000;
        Integer[] arr = ArrayGenerator.generateRandomArray(n, n);
        Integer[] arr2 = Arrays.copyOf(arr, arr.length);

        SortingHelper.sortTest("MergeSort", arr);
        SortingHelper.sortTest("QuickSort", arr2);

        Integer[] arr3 = ArrayGenerator.generateOrderedArray(n);
        Integer[] arr4 = Arrays.copyOf(arr3, arr3.length);

        SortingHelper.sortTest("MergeSort", arr3);
        SortingHelper.sortTest("QuickSort", arr4);


    }

}

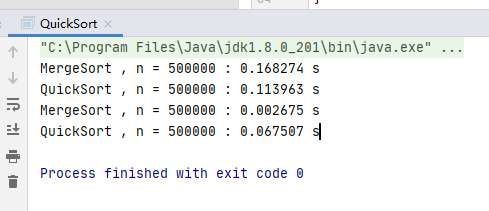
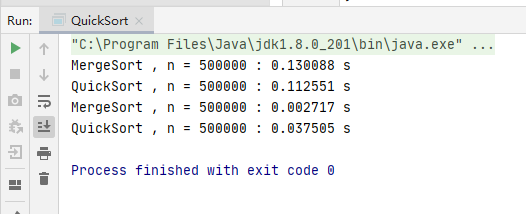
优化前的快速排序时间

优化后的快速排序时间

温馨提示

额，在我电脑上，快速排序还是输了[aru_34]

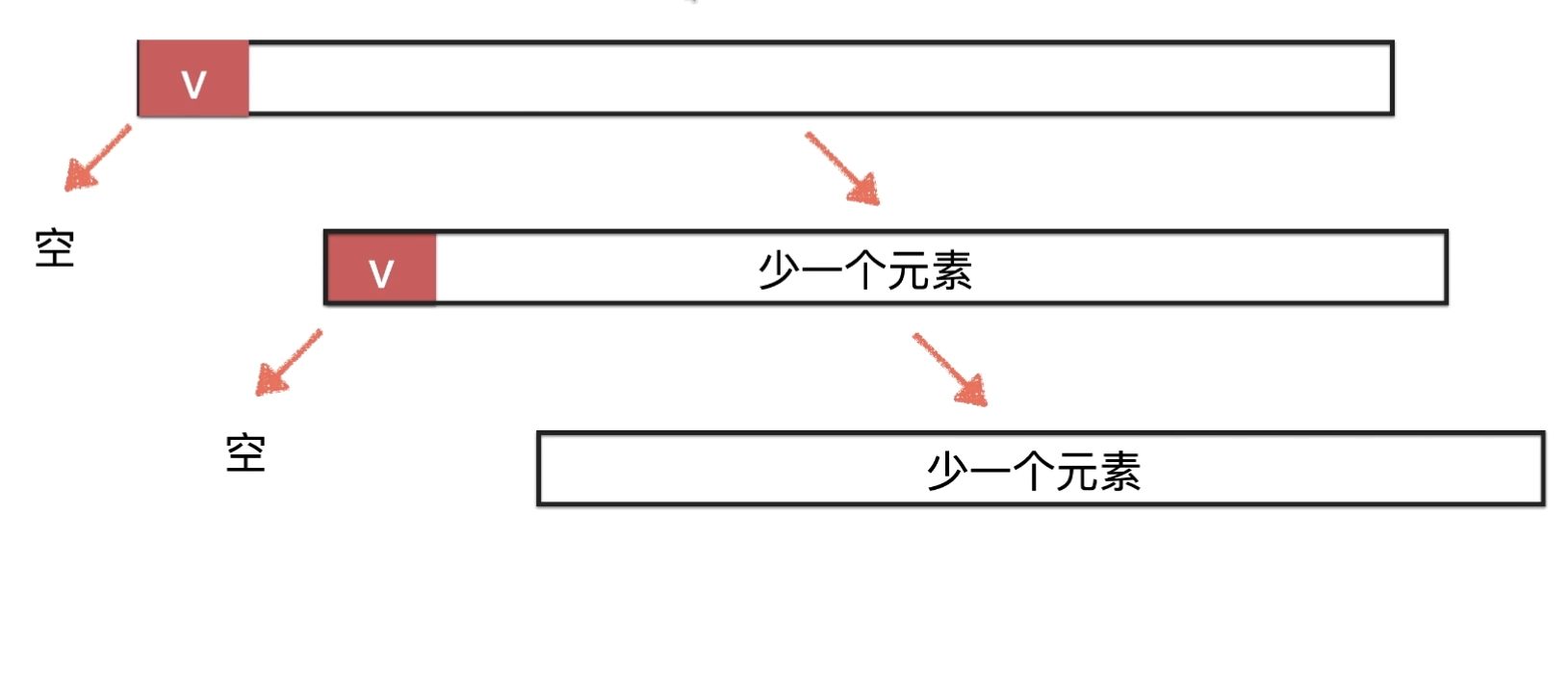
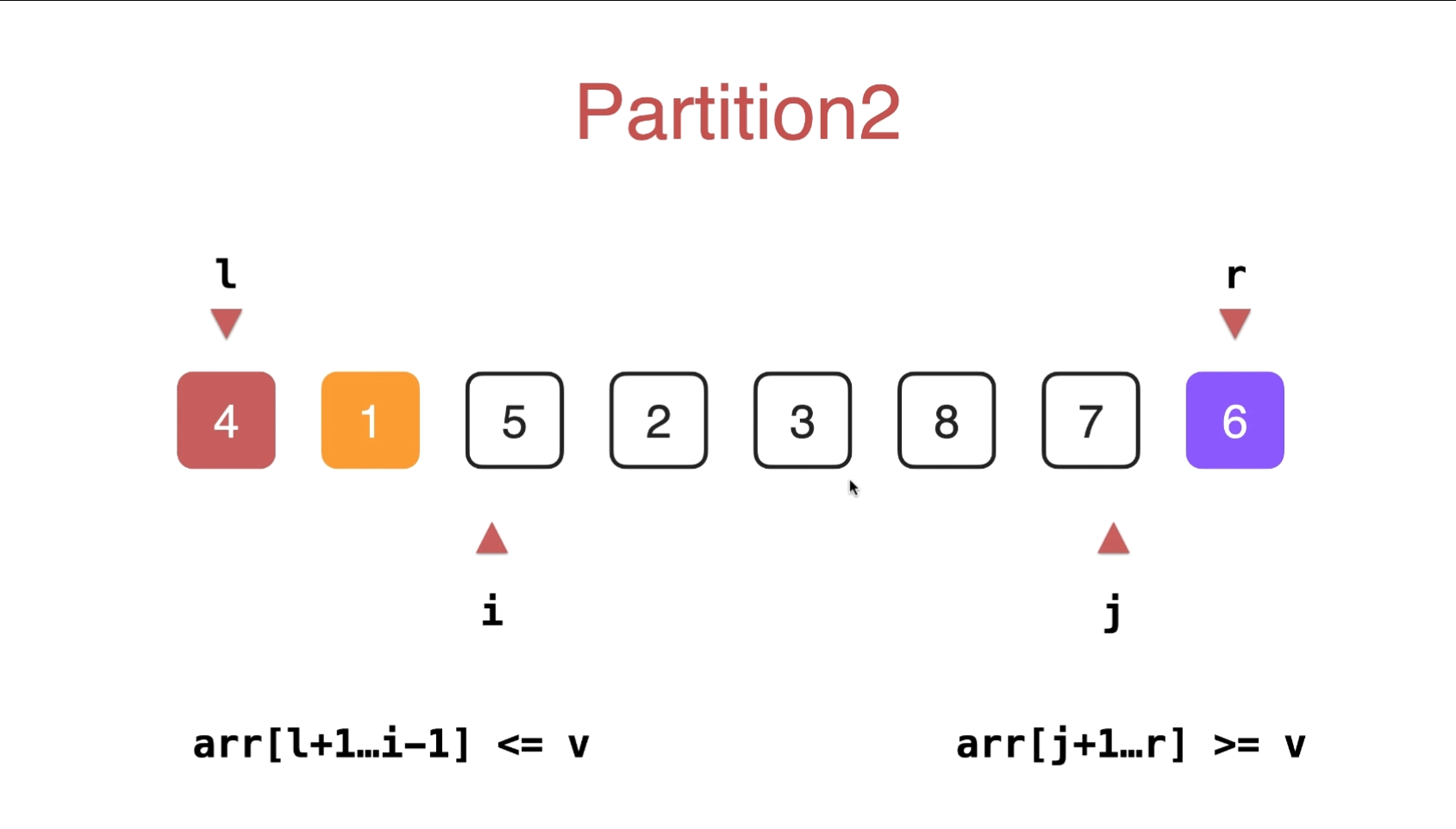
四、双路快速排序算法

温馨提示

继续优化我们的快速排序算法，今天来搞一个双路快速排序算法。
我们之前的第一版排序算法，在面对完全一样值的数组的时候，算法的时间复杂度会退化为O(n^2)级别，而我们这个新的快速排序算法就不会有这个问题啦

原理大话解读

温馨提示

i标识一直递增目的是找到小于标定点（这里是4）的值，j标识一直递减，目的找到大于标定点的值，双方都找到不是满足前面说的条件时候，将两个值进行交换，然后继续寻找，以此类推，然后就可以实现和上面的第一版快速排序算法partition一样的结果，以标定点为中心的左右两个数组（左数组都比标定点小，右数组都比标定点大），然后依次递归就完成了排序

核心代码

    public static <E extends Comparable<E>> void sort2ways(E[] arr) {
        Random rnd = new Random();
        sort2ways(arr, 0, arr.length - 1, rnd);
    }

    private static <E extends Comparable<E>> void sort2ways(E[] arr, int l, int r, Random rnd) {
        if (l >= r) {
            return;
        }
        int p = partition2(arr, l, r, rnd);
        sort2ways(arr, l, p - 1, rnd);
        sort2ways(arr, p + 1, r, rnd);
    }

    private static <E extends Comparable<E>> int partition2(E[] arr, int l, int r, Random rnd) {
        // 生成[l,r] 之间的随机索引
        int p = l + rnd.nextInt(r - l + 1);
        swap(arr, l, p);

        // arr[l+1...i-1] <= v; arr[j+1...r] >=v
        int i = l + 1, j = r;
        while (true) {
            while (i <= j && arr[i].compareTo(arr[l]) < 0) {
                i++;
            }
            while (j >= i && arr[j].compareTo(arr[l]) > 0) {
                j--;
            }
            if (i >= j) {
                break;
            }
            swap(arr, i, j);
            i++;
            j--;
        }
        swap(arr, l, j);
        return j;
    }

完整代码

点击查看完整内容

package quicksort;

import LinearSearch.ThreadDemo4;
import List.Array;
import MergeSort.ArrayGenerator;
import MergeSort.SortingHelper;

import java.util.Arrays;
import java.util.Random;
import java.util.concurrent.*;

public class QuickSort {
    private static final int CORE_POOL_SIZE = 5;
    private static final int MAX_POOL_SIZE = 10;
    private static final int QUEUE_CAPACITY = 100;
    private static final Long KEEP_ALIVE_TIME = 1L;

    private QuickSort() {
    }

    public static <E extends Comparable<E>> void sort(E[] arr) {
        Random rnd = new Random();
        sort(arr, 0, arr.length - 1, rnd);
    }

    private static <E extends Comparable<E>> void sort(E[] arr, int l, int r, Random rnd) {
        if (l >= r) {
            return;
        }
        int p = partition(arr, l, r, rnd);
        sort(arr, l, p - 1, rnd);
        sort(arr, p + 1, r, rnd);
    }

    private static <E extends Comparable<E>> int partition(E[] arr, int l, int r, Random rnd) {
        // 生成[l,r] 之间的随机索引
        int p = l + rnd.nextInt(r - l + 1);
        swap(arr, l, p);
        // arr[l+1...j] < v; arr[j+1...i] >= v
        int j = l;
        for (int i = l + 1; i <= r; i++) {
            if (arr[i].compareTo(arr[l]) < 0) {
                j++;
                swap(arr, i, j);
            }
        }
        swap(arr, l, j);
        return j;
    }


    public static <E extends Comparable<E>> void sort2ways(E[] arr) {
        Random rnd = new Random();
        sort2ways(arr, 0, arr.length - 1, rnd);
    }

    private static <E extends Comparable<E>> void sort2ways(E[] arr, int l, int r, Random rnd) {
        if (l >= r) {
            return;
        }
        int p = partition2(arr, l, r, rnd);
        sort2ways(arr, l, p - 1, rnd);
        sort2ways(arr, p + 1, r, rnd);
    }

    private static <E extends Comparable<E>> int partition2(E[] arr, int l, int r, Random rnd) {
        // 生成[l,r] 之间的随机索引
        int p = l + rnd.nextInt(r - l + 1);
        swap(arr, l, p);

        // arr[l+1...i-1] <= v; arr[j+1...r] >=v
        int i = l + 1, j = r;
        while (true) {
            while (i <= j && arr[i].compareTo(arr[l]) < 0) {
                i++;
            }
            while (j >= i && arr[j].compareTo(arr[l]) > 0) {
                j--;
            }
            if (i >= j) {
                break;
            }
            swap(arr, i, j);
            i++;
            j--;
        }
        swap(arr, l, j);
        return j;
    }

    /**
     * 简单的数组元素交换
     *
     * @param arr
     * @param i
     * @param j
     * @param <E>
     */
    private static <E> void swap(E[] arr, int i, int j) {
        E t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;

    }

    public static void main(String[] args) {
        int n = 100000;
        Integer[] arr = ArrayGenerator.generateRandomArray(n, n);
        Integer[] arr2 = Arrays.copyOf(arr, arr.length);

        System.out.println("乱序数组");
        SortingHelper.sortTest("QuickSort", arr);
        SortingHelper.sortTest("QuickSort2", arr2);

        Integer[] arr3 = ArrayGenerator.generateOrderedArray(n);
        Integer[] arr4 = Arrays.copyOf(arr3, arr3.length);

        System.out.println("有序数组");
        SortingHelper.sortTest("QuickSort", arr3);
        SortingHelper.sortTest("QuickSort2", arr4);

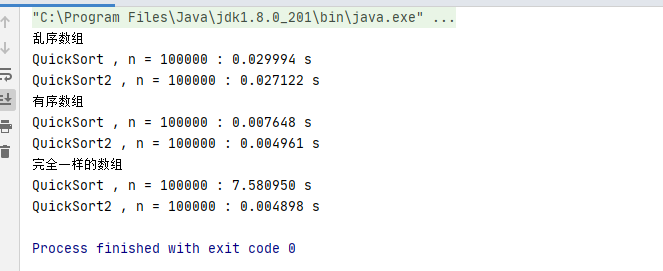
        System.out.println("完全一样的数组");
        Integer[] arr5 = ArrayGenerator.generateRandomArray(n,1);
        Integer[] arr6 = Arrays.copyOf(arr5, arr5.length);
        SortingHelper.sortTest("QuickSort", arr5);
        SortingHelper.sortTest("QuickSort2", arr6);


    }

}

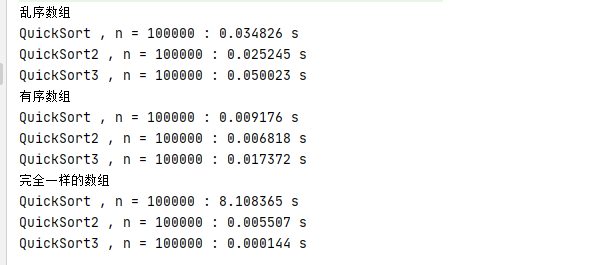
结果输出

温馨提示

可以看到，在完全值一样的情况下，我们的第一版快速排序算法居然那么垃圾！ [aru_42]

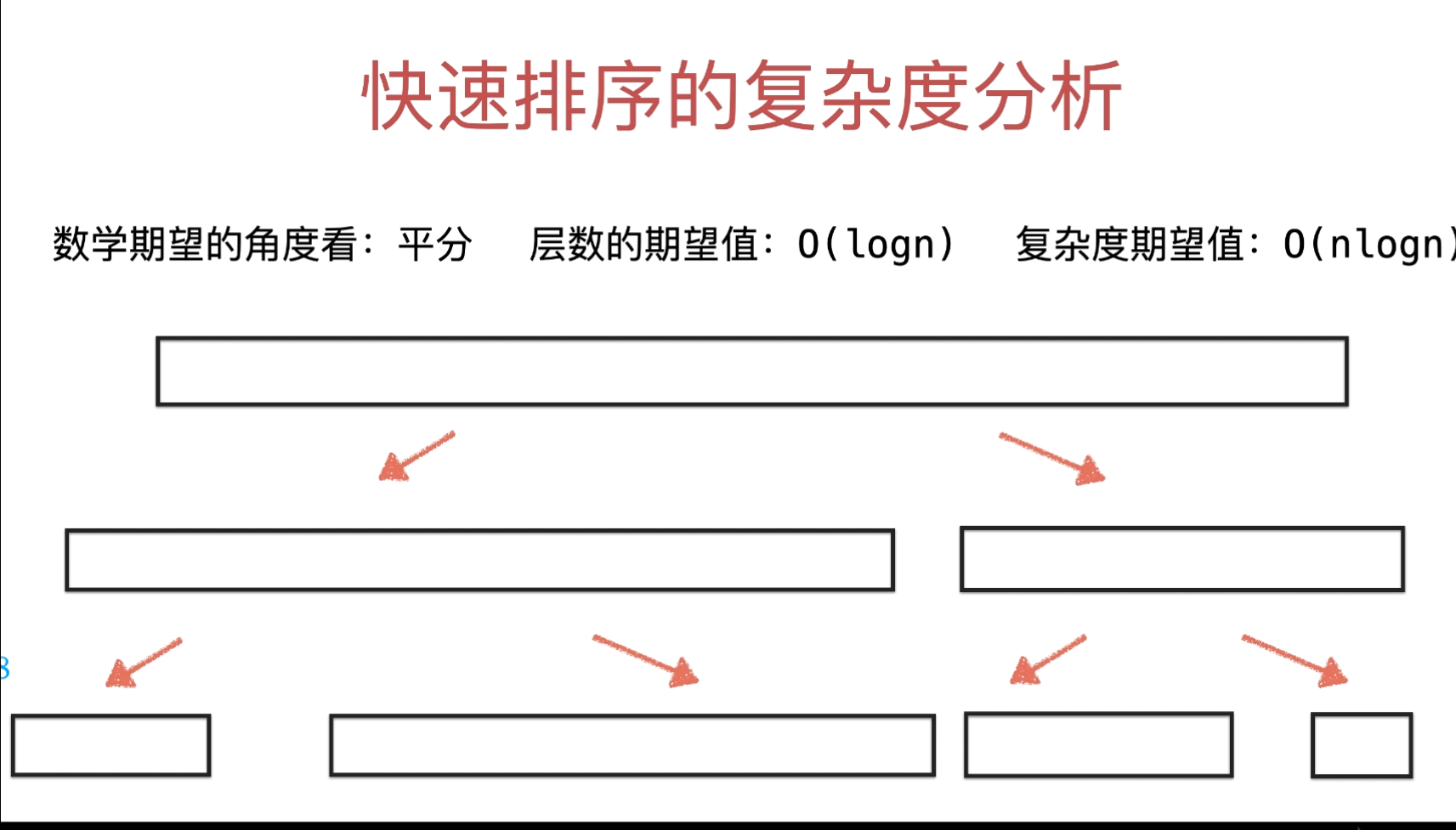
五、快速排序的复杂度分析

温馨提示

最恶劣的情况快速排序算法是O(n^2)，但是我们也知道，这种概率低到几乎可以忽略掉，我们的算法是一种随机算法，所以我们应该看一种可能的平均值来判断我们的选择排序算法。这是从一种数学期望的情况来看的

普通算法：看最差
- 能找到一组数据100%恶化
随机算法：看期望
- 不能找到一组数据100%恶化
多次调用？
- 尝试均摊分析

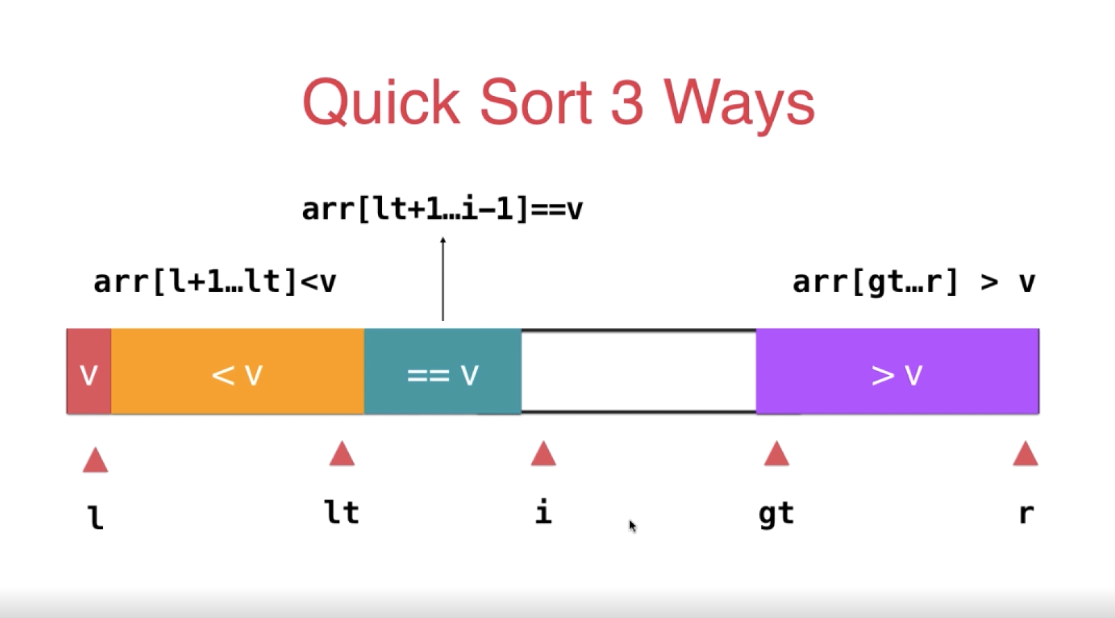
六、三路排序算法

温馨提示

和上面的两路排序算法思路差不多，我们看看关键代码就好啦！在这个算法的加持下，在完全相同的数组，他会进化为一个O(n)级别的算法，如果有很多相同的值，那么提升会非常明显的！

先看一张图，了解我们自定义的标识

关键代码

   public static <E extends Comparable<E>> void sort3ways(E[] arr) {
        Random rnd = new Random();
        sort3ways(arr, 0, arr.length - 1, rnd);
    }

    private static <E extends Comparable<E>> void sort3ways(E[] arr, int l, int r, Random rnd) {
        if (l >= r) {
            return;
        }
        // 生成 【l，r】 之间的随机索引
        int p = l + rnd.nextInt(r - l + 1);
        swap(arr, l, p);
        // arr[l+1,lt] < v,arr[lt+1,i-1] ==v,arr[gt,r]>v
        int lt = l, i = l + 1, gt = r + 1;
        while (i < gt) {
            if (arr[i].compareTo(arr[l]) < 0) {
                lt++;
                swap(arr, i, lt);
                i++;
            } else if (arr[i].compareTo(arr[l]) > 0) {
                gt--;
                swap(arr, i, gt);
            } else {
                //arr[i] == arr[l]
                i++;
            }
        }
        swap(arr, l, lt);
        // arr[l,lt-1]<v,arr[lt,gt-1]==v,arr[gt,r]>v
        sort3ways(arr, l, lt - 1, rnd);
        sort3ways(arr, gt, r, rnd);
    }

控制台输出

温馨提示

我们可以看到，在数组中的值完全一样的情况下，三路排序算法的优化效率还是比较明显的！

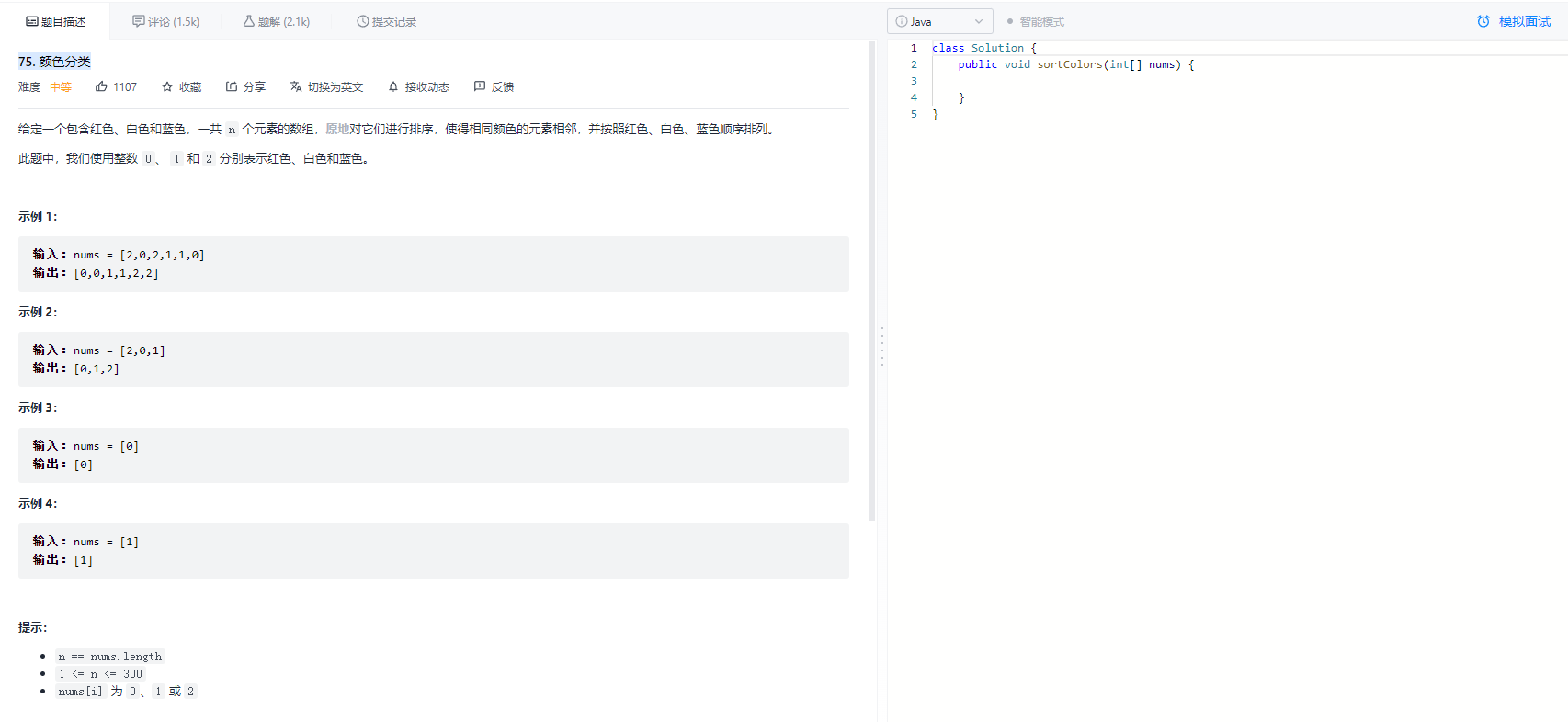
七、力扣题目——75. 颜色分类

具体题目

温馨提示

我们可以清晰的了解到题目的意思，我们可以使用简单的排序算法，都可以随便的解决，这里我们要想的是，我们可不可以使用三路排序算法，让这个算法的时间复杂度为O（n）级别呢？说干就干！

解析（引用慕课算法名师——波波老师）

- 实际上，这个问题是非常典型的，可以使用三路快速排序的partition思想解决的问题。因为，整个数组中只有0,1,2三种元素。如果我们把1当做标定点的话，就自然而然的可以把元素0当做是小于标定点的部分，元素2当做是大于标定点的部分。
- 所以，大家可以看出来，只要我们使用1当做标定点，只需要运行一遍三路快速排序的partition过程，就能完成任务了。
- 注意，在这个过程中，我们不需要随机去选择标定点了，我们已经通过对问题的分析，明确了标定点就是1.同时，我们也不需要一定把一个1放在数组的最左边。既然我们明确了标定点是1，在算法循环过程中，每个待处理的元素，直接和1进行比较就好了。
- 在下面的代码中，循环不变量的定义是：
  - - ```
    nums[0...zero] == 0
    nums[zero + 1,i - 1] == 1
    nums[two,n - 1] == 2
```
- 其实，变量zero相当于我们在三路快速排序算法中的lt；变量two相当于我们在三路快速排序算法中的gt。有了这个定义，相信理解了快速排序算法的partition的逻辑。

具体代码

class Solution {
    public void sortColors(int[] nums) {
        // nums[0...zero] == 0,nums[zero + 1, i] == 1,num[two,n - 1] == 2
        int zero = -1, i = 0, two = nums.length;
        while (i < two) {
            if (nums[i] == 0) {
                zero++;
                swap(nums, zero, i);
                i++;
            } else if (nums[i] == 2) {
                two--;
                swap(nums, i, two);
            } else {
                // nums[i] == 0;
                i++;
            }
        }
    }

    private void swap(int[] nums, int i, int j) {
        int t = nums[i];
        nums[i] = nums[j];
        nums[j] = t;
    }
}

可以看到是没有问题的

八、经典selectK题目

我们首先来封装一个selectK的方法。我们的selectK的接口是这样的

// 在arr[l...r] 的范围里求解整个数组的第k小元素并返回
// k 是索引，即从0开始计算
int selectK(int[] arr,int l,int r,int k,Random rnd)

因为我们的partition 过程需要随机选取标定点，所以我们还需要传一个Random 类的对象rnd。
定义好函数签名以后，下面我们来书写相应的逻辑
首先，selectK的过程，我们就是要执行一遍partition，在这个，我们使用双路快速排序的partition。
注意，因为在这个问题中，我们肯定我们处理的数据类型是int，所以，在代码中，我们将不再使用泛型：

    private int partition(int[] arr, int l, int r, Random rnd) {
        // 生成[l,r] 之间的随机索引
        int p = l + rnd.nextInt(r - l + 1);
        swap(arr, l, p);

        //arr[l+1...i-1] <= v; arr[j+1...r] >= v
        int i = l + 1, j = r;
        while (true) {
            while (i <= j && arr[i] < arr[l]) {
                i++;
            }
            while (j >= i && arr[j] > arr[l]) {
                j--;
            }
            if (i >= j) {
                break;
            }
            swap(arr, i, j);
            i++;
            j--;
        }
        swap(arr, l, j);
        return j;
    }

    private void swap(int[] arr, int i, int j) {
        int t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;
    }

有了partition，我们的selectK的主题逻辑非常简单。
首先，进行partition，假设结果是p，我们只需要将k和p作比较。
- 如果k==p，直接返回arr[p]即可。
- 如果k<p，在arr[l,p-1]的范围继续找，即调用selectK（arr,l,p-1,k,rnd）；
- 如果k>p，在arr[p+1,r]的范围继续找，即调用selectK（arr,p+1,r,k,rnd）；

关键selectK代码

    private int selectK(int[] arr, int l, int r, int k, Random rnd) {
        int p = partition(arr, l, r, rnd);
        if (k == p) {
            return arr[p];
        }
        if (k < p) {
            return selectK(arr, l, p - 1, k, rnd);
        }
        return selectK(arr, p + 1, r, k, rnd);

    }

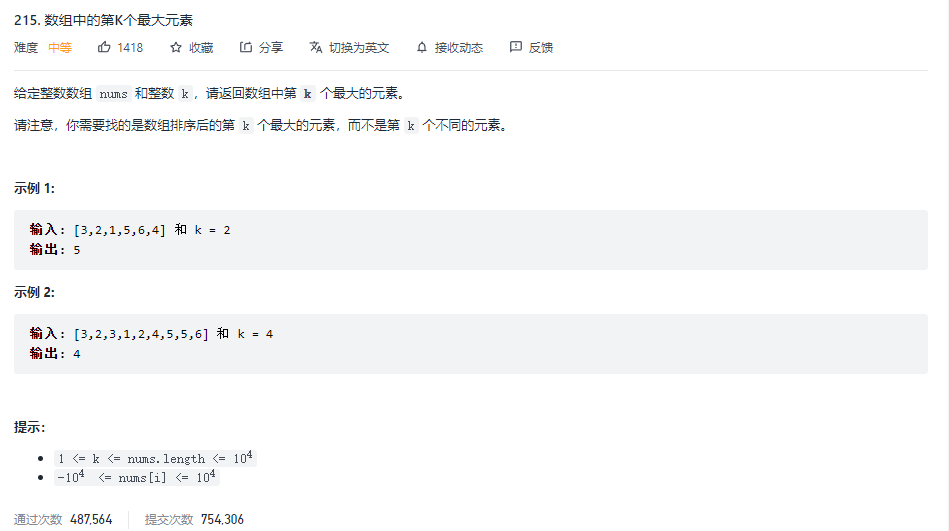
我们来看下面这题——力扣215题

温馨提示

这个问题是求第k大元素，但是我们的selectK求的是第k小元素怎么办？
我们只需要在调用selectK之前，将求第k大元素的这个k，转换成对应求得是低级小元素对应的索引就好了。
按照题目描述，如果k是l，对应的就是要找最大元素，那么相应的我们selectK的索引就是nums.length - 1.
如果k是nums.length,其实就是求最小元素，那么相应我们的selectK的索引就是0
他们之间的转换关系是nums.length - 1
所以，对于这个问题，我们的代码关键如下

    public int findKthLargest(int[] nums, int k) {
        Random rnd = new Random();
        return selectK(nums, 0, nums.length - 1, nums.length - k, rnd);
    }

完整代码

点击查看完整内容

package solution3;

import java.util.Random;

class Solution {
    public int findKthLargest(int[] nums, int k) {
        Random rnd = new Random();
        return selectK(nums, 0, nums.length - 1, nums.length - k, rnd);
    }

    private int selectK(int[] arr, int l, int r, int k, Random rnd) {
        int p = partition(arr, l, r, rnd);
        if (k == p) {
            return arr[p];
        }
        if (k < p) {
            return selectK(arr, l, p - 1, k, rnd);
        }
        return selectK(arr, p + 1, r, k, rnd);

    }

    private int partition(int[] arr, int l, int r, Random rnd) {
        // 生成[l,r] 之间的随机索引
        int p = l + rnd.nextInt(r - l + 1);
        swap(arr, l, p);

        //arr[l+1...i-1] <= v; arr[j+1...r] >= v
        int i = l + 1, j = r;
        while (true) {
            while (i <= j && arr[i] < arr[l]) {
                i++;
            }
            while (j >= i && arr[j] > arr[l]) {
                j--;
            }
            if (i >= j) {
                break;
            }
            swap(arr, i, j);
            i++;
            j--;
        }
        swap(arr, l, j);
        return j;
    }

    private void swap(int[] arr, int i, int j) {
        int t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;
    }
}

输出结果

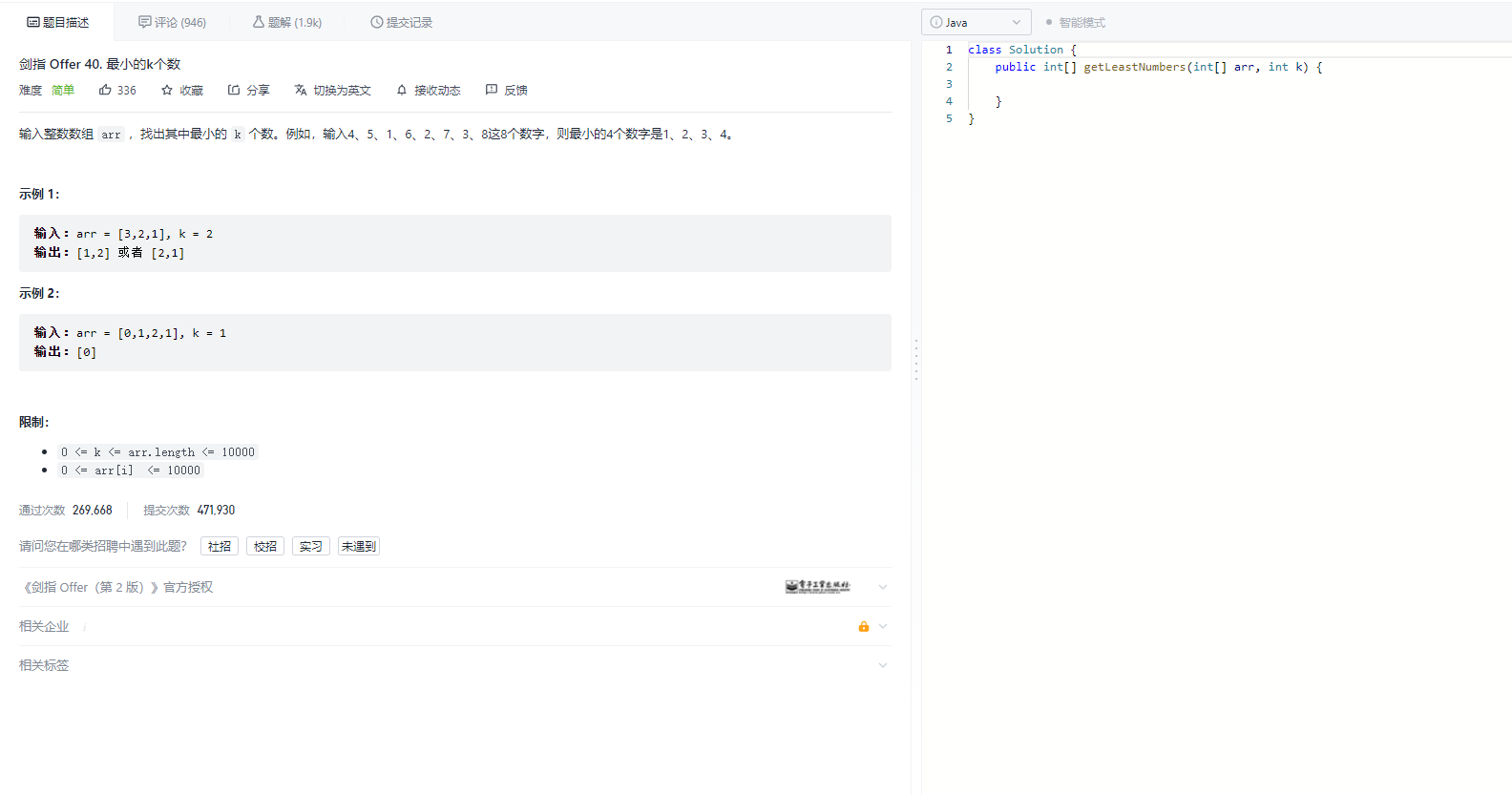
我们再来看一题，《剑指offer》——40题

温馨提示

对于这个问题，我们只要使用上面的selectK，找到第k小的数。然后，selectK的过程由于调用了partition，所以会调整整个数组的内容。此时，这个第k小的数前面的所有元素，就是整个数组最小的k个数字了。
这里要注意的是，我们求的第k小的数字，对应的索引是k-1，所以我们调用selectK的时候，需要传入的索引参数是k-1。
另外，对于这个问题，k可能取0，此时，我们不需要执行selectK，直接返回一个含有0个元素的int[]就好了。具体关键代码如下：

    public int[] getLeastNumbers(int[] arr, int k) {
        if (k == 0) {
            return new int[0];
        }
        Random rnd = new Random();
        selectK(arr, 0, arr.length - 1, k - 1, rnd);
        return Arrays.copyOf(arr, k);
    }

温馨提示

完整代码看上面的，这里不再重复了

结果输出

本文作者为DBC，转载请注明。

算法