归并排序法——递归加餐

DBC 1.8K 0

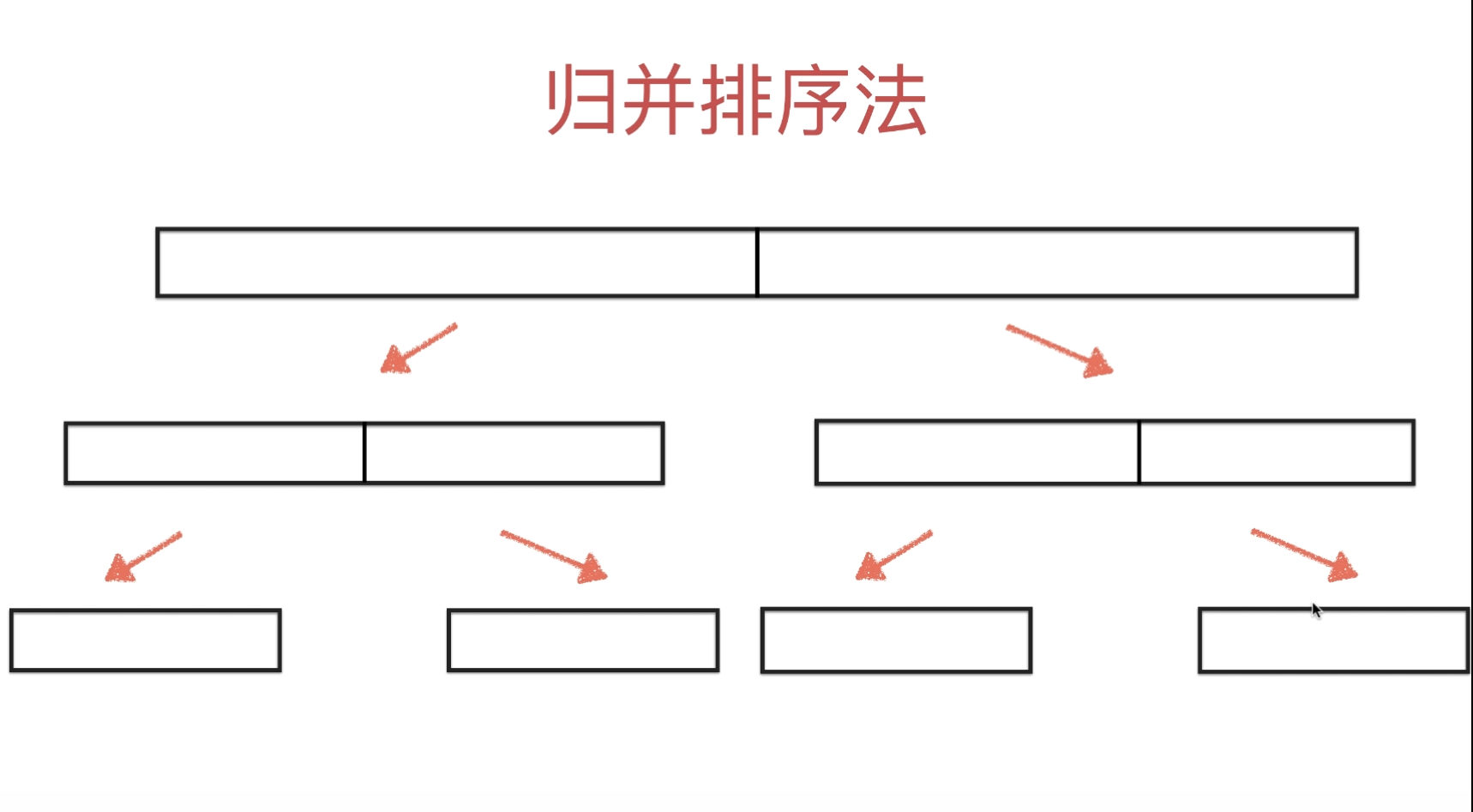
一、归并排序法的原理

归并排序法——递归加餐插图

温馨提示

简单来说：我们将一个大数组分为小数组然后再排好序，层层分小数组并且排好序再拼装起来
小知识：归并的过程无法原地完成

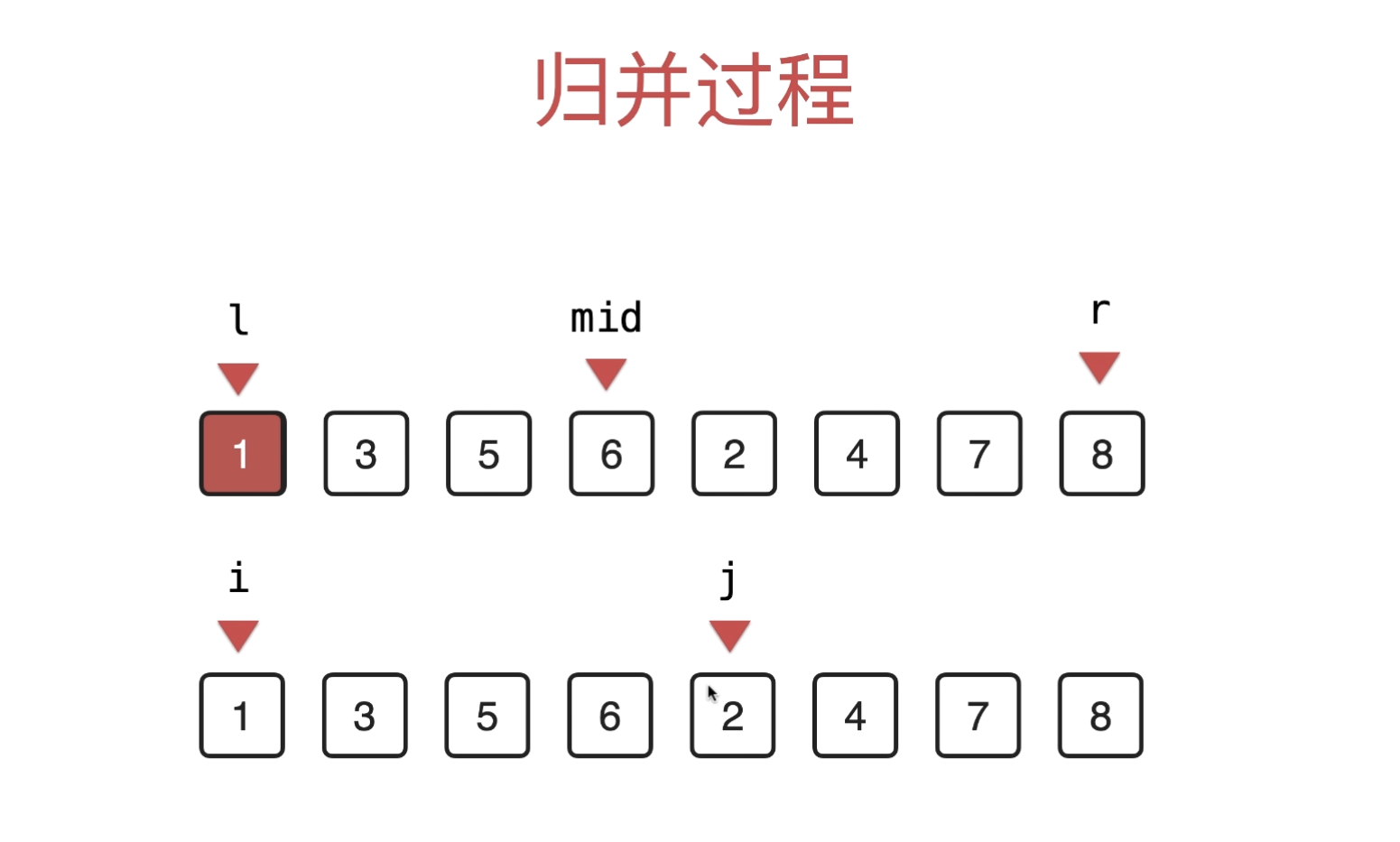
归并过程一览（了解l、r、mid是什么意思）

归并排序法——递归加餐插图2

  • mid 什么意思？
    • ( l + r)/2 = (0 + 7)/2  ≈3
    • mid = 3

三、实现归并过程操作

    // 合并两个有序的区间 arr[l,mid] 和 arr[mid+1,r]
    private static <E extends Comparable<E>> void merge(E[] arr, int l, int mid, int r) {
        E[] temp = Arrays.copyOfRange(arr, l, r + 1);
        int i = l, j = mid + 1;
        //每轮循环为 arr[k]赋值
        for (int k = l; k <= r; k++) {
            if (i > mid) {
                arr[k] = temp[j - l];
                j++;
            }else if (j>r){
                arr[k] = temp[i-l];
                i++;
            }else if(temp[i-l].compareTo(temp[j-l])<=0){
                arr[k] = temp[i-l];
                i++;
            }else {
                arr[k] = temp[j-l];
                j++;
            }
            // arr[i] 和 arr[j]
        }
    }

四、实现归并排序算法操作

完整代码

public class MergeSort {
    private MergeSort() {
    }
    public static <E extends Comparable<E>> void sort(E[] arr) {
        sort(arr, 0, arr.length - 1);
    }

    private static <E extends Comparable<E>> void sort(E[] arr, int l, int r) {
        if (l >= r) {
            return;
        }
        //int mid = (l + r) / 2;
        //上亿级别的数组需要这样优化
        int mid = l + (r - l) / 2;
        sort(arr, l, mid);
        sort(arr, mid + 1, r);
        merge(arr, l, mid, r);
    }

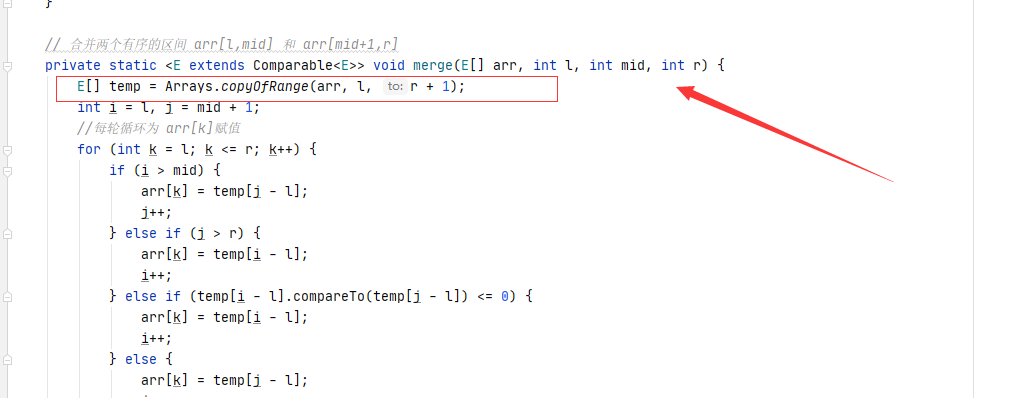
    // 合并两个有序的区间 arr[l,mid] 和 arr[mid+1,r]
    private static <E extends Comparable<E>> void merge(E[] arr, int l, int mid, int r) {
        E[] temp = Arrays.copyOfRange(arr, l, r + 1);
        int i = l, j = mid + 1;
        //每轮循环为 arr[k]赋值
        for (int k = l; k <= r; k++) {
            if (i > mid) {
                arr[k] = temp[j - l];
                j++;
            } else if (j > r) {
                arr[k] = temp[i - l];
                i++;
            } else if (temp[i - l].compareTo(temp[j - l]) <= 0) {
                arr[k] = temp[i - l];
                i++;
            } else {
                arr[k] = temp[j - l];
                j++;
            }
            // arr[i] 和 arr[j]
        }
    }

    public static void main(String[] args) {
        int n = 100000;
        Integer[] arr = ArrayGenerator.generateRandomArray(n,n);
        SortingHelper.sortTest("MergeSort",arr);
    }
}

控制台输出

归并排序法——递归加餐插图4

五、归并算法的复杂度分析

首先我们先来看三个排序具体所需要的时间（归并排序法、选择排序法、冒泡排序法），如下图：

归并排序法——递归加餐插图6

温馨提示

我们可以非常直观的看到它们之间的区别，归并算法这个速度，我只能说无敌（尽管我们没有进行优化），真的是逆天级别！这就是算法的魅力吗？ [aru_49]
这种算法的速度上面，是那两个排序法（没错，说的就是选择、冒泡排序）无论如何优化代码也赶不上的差距！！！！[aru_59]

归并排序法复杂度为——O（nlogn）级别

随着n的逐渐加大，那么这个时间会越来越大！时间差异将会大得恐怖！

温馨提示

举例一个简单的例子：假设数据有100000；那么n^2和nlogn之间的差距会有6020倍！！！这是什么概念，也就是如果归并用一天才能算出来的数据，那么。。其他需要6020天，是多少？[aru_34]
这就是我们学习算法的意义！[aru_42]

六、对归并算法的优化操作

判断是否需要排序才进行合并操作，具体看下面的代码

    private static <E extends Comparable<E>> void sort2(E[] arr, int l, int r) {
        if (l >= r) {
            return;
        }
        //int mid = (l + r) / 2;
        //上亿级别的数组需要这样优化
        int mid = l + (r - l) / 2;
        sort(arr, l, mid);
        sort(arr, mid + 1, r);

        if (arr[mid].compareTo(arr[mid+1])>0){
            merge(arr, l, mid, r);
        }

    }

关键代码

        if (arr[mid].compareTo(arr[mid+1])>0){
            merge(arr, l, mid, r);
        }

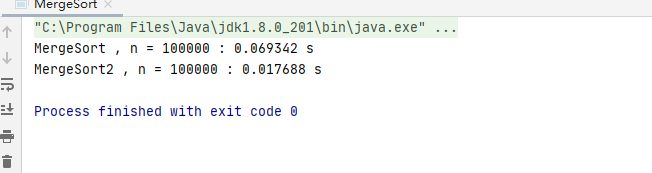
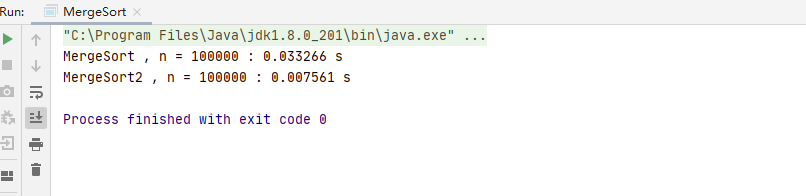
控制台输出

归并排序法——递归加餐插图8

温馨提示

我们可以看到，其优化效果是非常不错的！

当我们如果是完全有序的数组，我们的速度将会更快！具体如下图

归并排序法——递归加餐插图10

小知识

如我们上面那样，对merge进行判断之后，对完全有序的数组归并排序是O（n）级别，插入排序法对完全有序的数组也是O（n）级别的（正常是O（n^2））。

七、使用插入排序算法来优化归并排序算法

优化思想：在比较小的数组排序中，我们使用插入排序法可能会让代码排序的效率更加的高效，具体代码如下，这里没有给出完全的插入排序算法代码，只有关键代码，具体可以查看我插入排序算法的文章

    private static <E extends Comparable<E>> void sort2(E[] arr, int l, int r) {

        if (r-l<=15){
            InsertionSort.sort3(arr,l,r);
        }
        //上亿级别的数组需要这样优化
        int mid = l + (r - l) / 2;
        sort(arr, l, mid);
        sort(arr, mid + 1, r);
        merge(arr, l, mid, r);
        if (arr[mid].compareTo(arr[mid+1])>0){
            merge(arr, l, mid, r);
        }

    }

可以看到，我们对于长度小于等于15的数组，直接调用了插入排序算法的代码，如下

    public static <E extends Comparable<E>> void sort3(E[] arr,int l,int r) {
        for (int i = 0; i <= r; i++) {
            //将 arr[i] 插入到合适的位置
            E t = arr[i];
            int j;
            for (j = i; j - 1 >= l && t.compareTo(arr[j - 1]) < 0; j--) {
                arr[j] = arr[j-1];
            }
            arr[j] = t;
        }
    }

我们以50万长度数组来测试

归并排序法——递归加餐插图12

温馨提示

这里仅作为一个小知识储备，我们这样的操作在其他语言中可能会有反效果，所以我们后面的学习会将这个代码剔除，其实效果差距也不是很夸张。在面试的时候，我们知道还有这个思想就好了，说不定是一个加分项，哈哈哈[aru_12]

八、归并排序法的内存操作

具体操作思想：之前我们每次跑一下这个方法我们就重新创建一个数组，这样内存中的数据会非常的大，在长度很长的时候这是非常不友好的，我们修改一下，让我们只在内存中创建一次数组！

归并排序法——递归加餐插图14

具体代码如下

    public static <E extends Comparable<E>> void sort2(E[] arr) {
        E[] temp = Arrays.copyOf(arr, arr.length);
        sort2(arr, 0, arr.length - 1, temp);
    }

    private static <E extends Comparable<E>> void sort2(E[] arr, int l, int r, E[] temp) {
        if (l >= r) {
            return;
        }
        //int mid = (l + r) / 2;
        //上亿级别的数组需要这样优化
        int mid = l + (r - l) / 2;
        sort2(arr, l, mid, temp);
        sort2(arr, mid + 1, r, temp);

        if (arr[mid].compareTo(arr[mid + 1]) > 0) {
            merge2(arr, l, mid, r, temp);
        }

    }

    // 合并两个有序的区间 arr[l,mid] 和 arr[mid+1,r]
    private static <E extends Comparable<E>> void merge2(E[] arr, int l, int mid, int r, E[] temp) {
        System.arraycopy(arr, l, temp, l, r - l + 1);
        int i = l, j = mid + 1;
        //每轮循环为 arr[k]赋值
        for (int k = l; k <= r; k++) {
            if (i > mid) {
                arr[k] = temp[j];
                j++;

            } else if (j > r) {
                arr[k] = temp[i];
                i++;

            } else if (temp[i].compareTo(temp[j]) <= 0) {
                arr[k] = temp[i];
                i++;

            } else {
                arr[k] = temp[j];
                j++;

            }
            // arr[i] 和 arr[j]
        }
    }

依然是50万长度的数组进行对比测试，如下图

归并排序法——递归加餐插图16

温馨提示

我们可以看到，其效果还是很明显的！这是一种正统的优化思想，需要好好理解哈！ [aru_55]

九、实现自底向上的归并排序

我们之前的 归并排序是从顶部一路下来的递归操作，现在我们来看一个自底向上的归并排序操作

    // 自底向上的归并排序
    static <E extends Comparable<E>> void sortBU(E[] arr) {
        E[] temp = Arrays.copyOf(arr, arr.length);
        int n = arr.length;
        // 遍历合并的区间长度
        for (int sz = 1; sz < n; sz += sz) {
            // 遍历合并的两个区间的起始位置 i
            // 合并 [i,i + sz - 1] 和 [i + sz ,Math.min(i + sz + sz - 1, n - 1)]
            for (int i = 0; i + sz < n; i += sz + sz) {
                if (arr[i+sz-1].compareTo(arr[i+sz])>0){
                    merge(arr, i,i + sz - 1, Math.min(i + sz + sz - 1, n - 1), temp);
                }
            }
        }

    }

控制台输出

归并排序法——递归加餐插图18

温馨提示

我们可以看到，两个操作的时间在伯仲之间，不过理论上说，应该是自底向上的排序会快于递归的排序！

十、数组中的逆序数对数量问题

什么是逆序数对

归并排序法——递归加餐插图20

温馨提示

简单来说，看上面的图7和1就是逆序数对，当然也不是相邻的才是，7和4等也是逆序数对，相信很清晰

那么问题来了，我们想要求一个数组中，含有多少个逆序数对，该怎么操作呢？

温馨提示

最简单的解决方案，就是暴力循环解决，双重循环，无脑遍历[aru_42]，但是，我们也知道，这样的操作是O（n^2)的级别

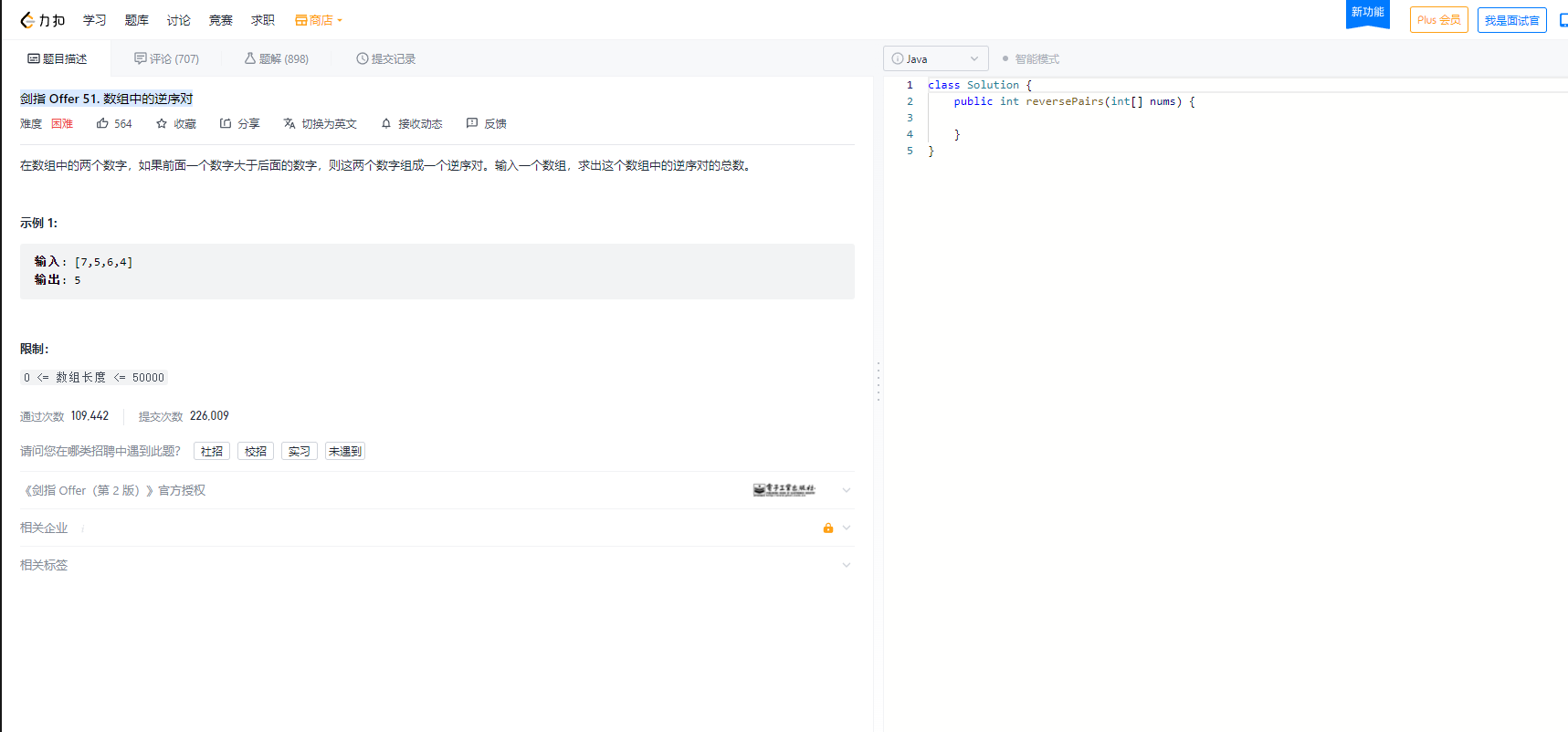
我们来看力扣的——剑指 Offer 51. 数组中的逆序对

具体如下

归并排序法——递归加餐插图22

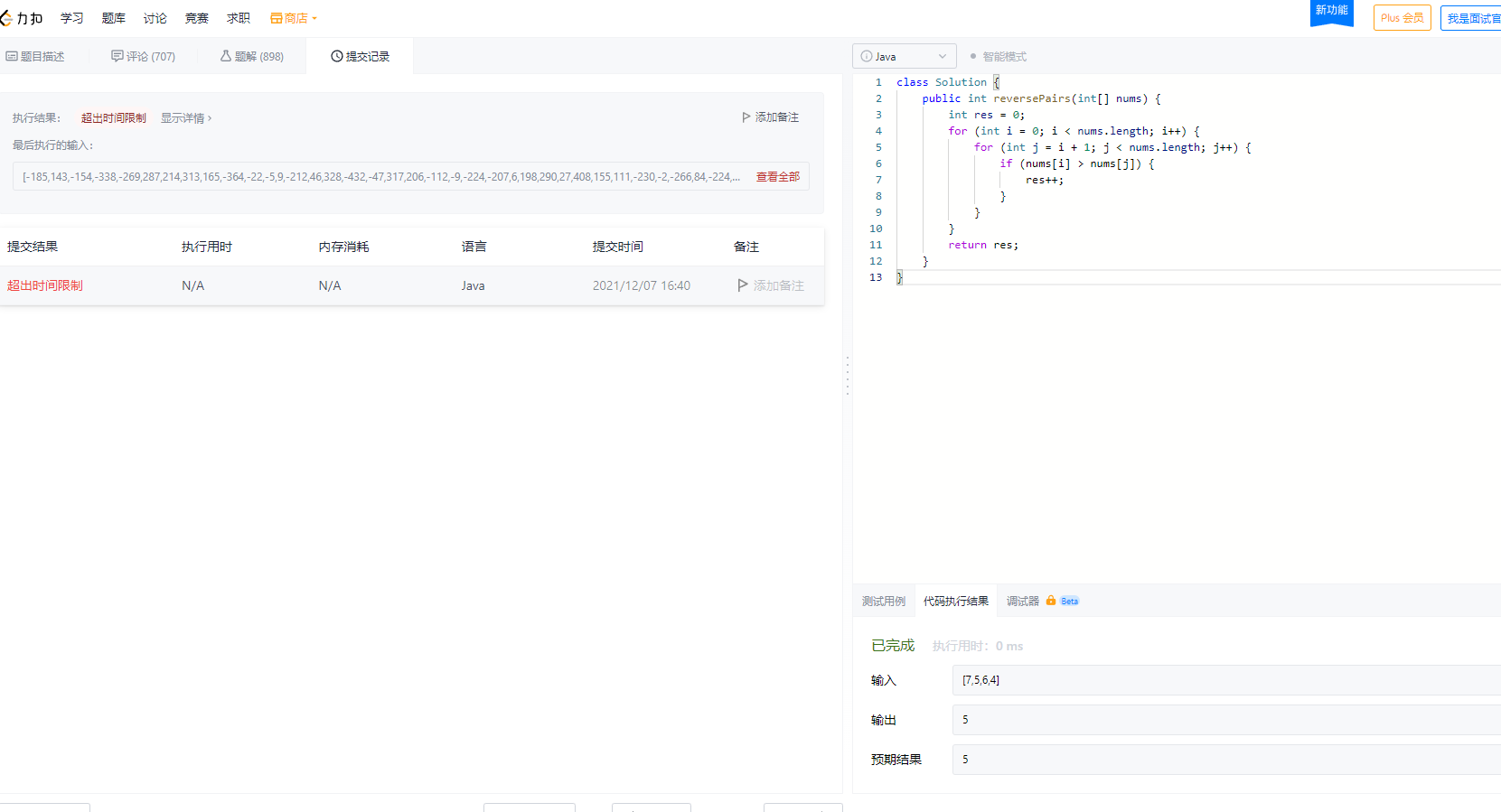
我们暴力代码提交力扣，看看什么情况

class Solution {
    public int reversePairs(int[] nums) {
        int res = 0;
        for (int i = 0; i < nums.length; i++) {
            for (int j = i + 1; j < nums.length; j++) {
                if (nums[i] > nums[j]) {
                    res++;
                }
            }
        }
        return res;
    }
}

归并排序法——递归加餐插图24

温馨提示

可以看到，输出结果是没有问题，但是提示我们超出了时间限制 [aru_35]

我们使用归并排序来帮助我们实现

package solution2;

class Solution {
    private int res = 0;

    public int reversePairs(int[] nums) {
        int[] temp = new int[nums.length];
        res = 0;
        sort(nums, 0, nums.length - 1, temp);
        return res;
    }


    private void sort(int[] arr, int l, int r, int[] temp) {
        if (l >= r) {
            return;
        }
        //int mid = (l + r) / 2;
        //上亿级别的数组需要这样优化
        int mid = l + (r - l) / 2;
        sort(arr, l, mid, temp);
        sort(arr, mid + 1, r, temp);

        if (arr[mid] > arr[mid + 1]) {
            merge(arr, l, mid, r, temp);
        }

    }

    // 合并两个有序的区间 arr[l,mid] 和 arr[mid+1,r]
    private void merge(int[] arr, int l, int mid, int r, int[] temp) {
        System.arraycopy(arr, l, temp, l, r - l + 1);
        int i = l, j = mid + 1;
        //每轮循环为 arr[k]赋值
        for (int k = l; k <= r; k++) {
            if (i > mid) {
                arr[k] = temp[j];
                j++;

            } else if (j > r) {
                arr[k] = temp[i];
                i++;

            } else if (temp[i] <= temp[j]) {
                arr[k] = temp[i];
                i++;

            } else {
                res += mid - i + 1;
                arr[k] = temp[j];
                j++;

            }
            // arr[i] 和 arr[j]
        }
    }


}

提交力扣代码

归并排序法——递归加餐插图26

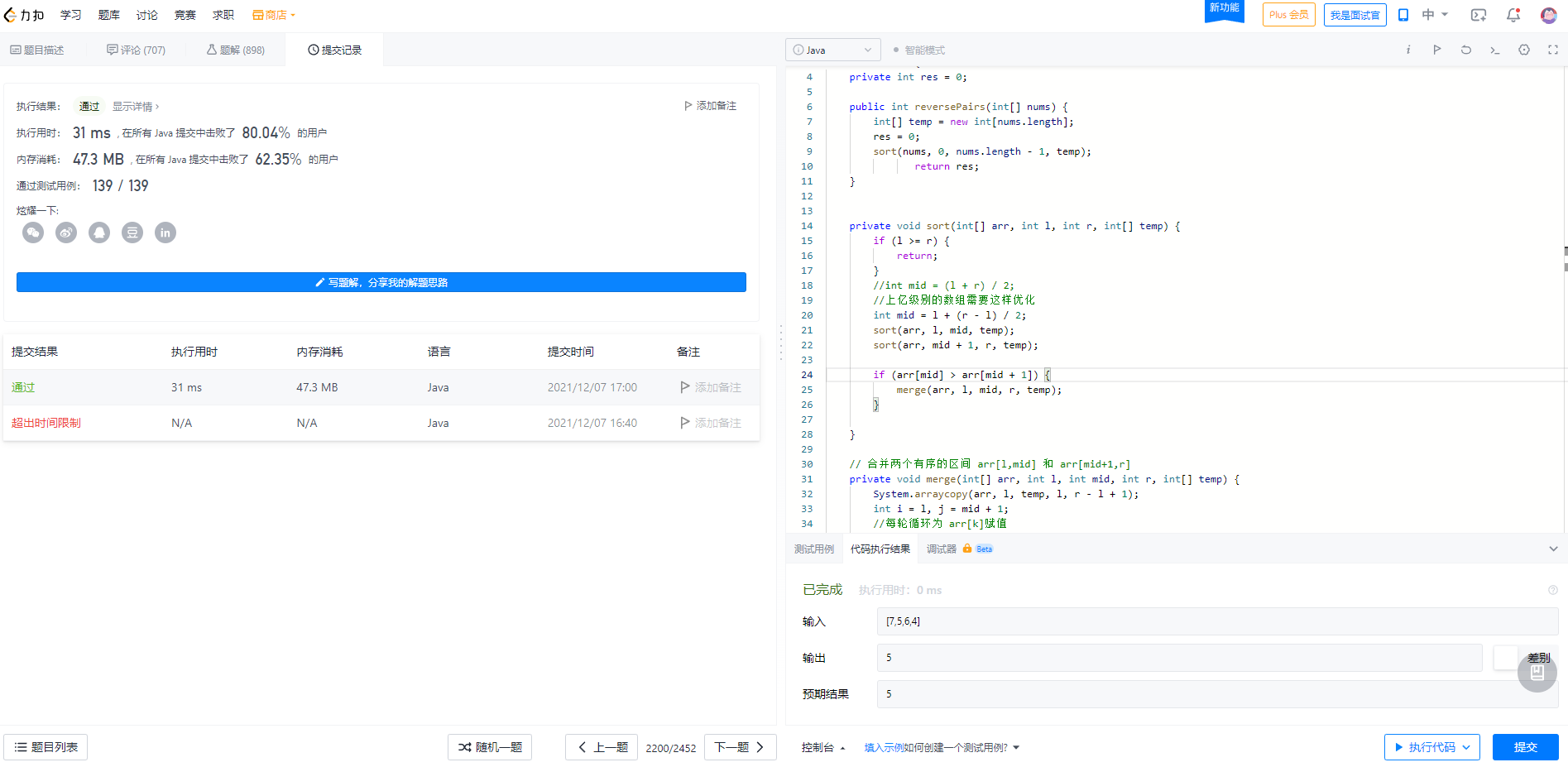
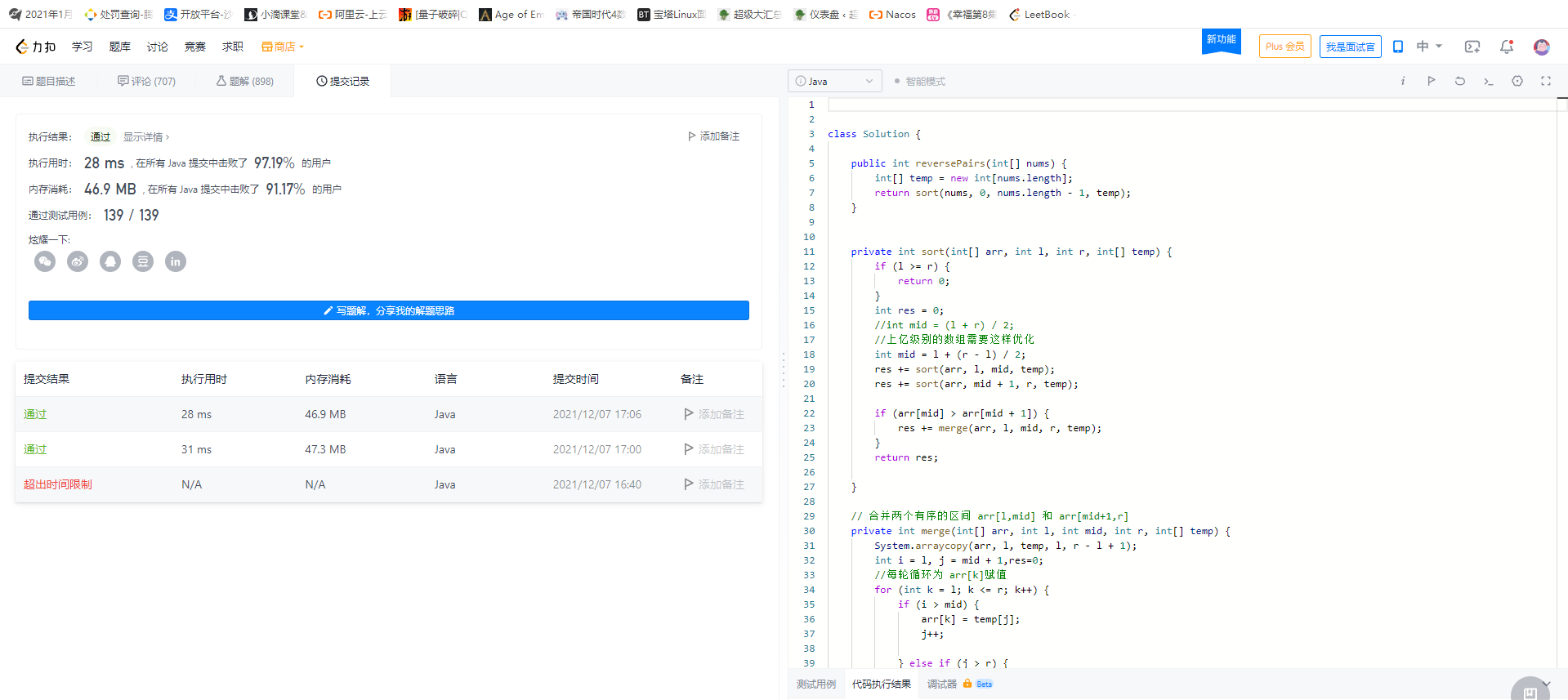
这里我们还可以有一种优化思想，因为我们定义了一个res，我们需要对它进行维护，那我们应该怎么优化呢？

package solution2;

class Solution {

    public int reversePairs(int[] nums) {
        int[] temp = new int[nums.length];
        return sort(nums, 0, nums.length - 1, temp);
    }


    private int sort(int[] arr, int l, int r, int[] temp) {
        if (l >= r) {
            return 0;
        }
        int res = 0;
        //int mid = (l + r) / 2;
        //上亿级别的数组需要这样优化
        int mid = l + (r - l) / 2;
        res += sort(arr, l, mid, temp);
        res += sort(arr, mid + 1, r, temp);

        if (arr[mid] > arr[mid + 1]) {
            res += merge(arr, l, mid, r, temp);
        }
        return res;

    }

    // 合并两个有序的区间 arr[l,mid] 和 arr[mid+1,r]
    private int merge(int[] arr, int l, int mid, int r, int[] temp) {
        System.arraycopy(arr, l, temp, l, r - l + 1);
        int i = l, j = mid + 1,res=0;
        //每轮循环为 arr[k]赋值
        for (int k = l; k <= r; k++) {
            if (i > mid) {
                arr[k] = temp[j];
                j++;

            } else if (j > r) {
                arr[k] = temp[i];
                i++;

            } else if (temp[i] <= temp[j]) {
                arr[k] = temp[i];
                i++;

            } else {
                res += mid - i + 1;
                arr[k] = temp[j];
                j++;

            }
            // arr[i] 和 arr[j]
        }
        return res;
    }


}
温馨提示

代码极其优雅，可以好好理解！

提交力扣

归并排序法——递归加餐插图28

本文作者为DBC，转载请注明。

发表评论 取消回复
表情 图片 链接 代码

分享