算法数据与结构——栈和队列

一、什么是栈？

二、栈的实现

代码实现

package stack;


public class Array<E> {
    private E[] data;
    private int size;

    //  构造函数，传入数组的容量capacity构造Array
    public Array(int capacity) {
        data = (E[]) new Object[capacity];
        size = 0;
    }

    //  无参数的构造函数，默认数组的容量capacity = 10
    public Array() {
        this(10);
    }

    //  获取数组中的元素个数
    public int getSize() {
        return size;
    }

    //  获取数组的容量
    public int getCapacity() {
        return data.length;
    }

    //  数组是否为空
    public boolean isEmpty() {
        return size == 0;
    }

    //  向所有元素后添加一个新元素
    public void addLast(E e) {
        add(size, e);
    }

    //在所有元素前添加一个元素
    public void addFirst(E e) {
        add(0, e);
    }

    //  在第index个位置插入一个新元素e
    public void add(int index, E e) {

        if (index < 0 || index > size)
            System.out.println("添加新元素方法失败，插入位置不可以为负数，也不可以大于数组长度");
        if (size == data.length)
            resize(2 * data.length);
        for (int i = size - 1; i >= index; i--) {
            data[i + 1] = data[i];
        }
        data[index] = e;
        size++;
    }

    // 扩容两倍
    private void resize(int newCapacity) {
        E[] newData = (E[]) new Object[newCapacity];
        for (int i = 0; i < size; i++)
            newData[i] = data[i];
        data = newData;
    }

    @Override
    public String toString() {
        StringBuilder res = new StringBuilder();
        res.append(String.format("Array: size = %d , capacity = %d\n", size, data.length));
        for (int i = 0; i < size; i++) {
            res.append(data[i]);
            if (i != size - 1)
                res.append(", ");
        }
        return res.toString();
    }

    //获取index索引位置的元素
    E get(int index) {
        if (index < 0 || index >= size)
            System.out.println("传入不合法！");
        return data[index];
    }

    //修改index索引位置的元素为e
    void set(int index, E e) {
        if (index < 0 || index >= size)
            System.out.println("传入不合法！");
        data[index] = e;
    }
    public E getLast(){
        return get(size - 1);
    }
    public E getFast(){
        return get(size - 1);
    }


    // 查找数组中是否有元素e
    public boolean contains(E e) {
        for (int i = 0; i < size; i++) {
            if (data[i].equals(e))
                return true;
        }
        return false;
    }

    //查找数组中元素e所在的索引，如果不存在元素e，则返回-1
    public int find(E e) {
        for (int i = 0; i < size; i++) {
            if (data[i].equals(e))
                return i;
        }
        return -1;
    }

    //从数组中删除index位置的元素，返回删除的元素
    public E remove(int index) {
        if (index < 0 || index >= size)
            System.out.println("传入不合法！");
        E ret = data[index];
        for (int i = index + 1; i < size; i++)
            data[i - 1] = data[i];
        size--;
        data[size] = null;  //loitering objects != memory leak

        //动态减小数组
        if (size == data.length / 4 && data.length / 2 !=0)
            resize(data.length / 2);
        return ret;
    }

    // 从数组中删除第一个元素，返回删除的元素
    public E removeFirst() {
        return remove(0);
    }

    //从数组中删除最后一个元素，返回删除的元素
    public E removeLast() {
        return remove(size - 1);
    }

    // 从数组中删除元素e
    public void removeElement(E e) {
        int index = find(e);
        if (index != -1)
            remove(index);
    }
}

package stack;

public class ArrayStack<E> implements Stack {
    Array<E> array;

    public ArrayStack(int capacity){
        array = new Array<E>(capacity);
    }
    public ArrayStack(){
        array = new Array<E>();
    }

    /**
     * 获取数组容量
     * @return
     */
    public int getCapacity(){
        return array.getCapacity();
    }
    @Override
    public int getSize() {
        return array.getSize();
    }

    @Override
    public boolean isEmpty() {
        return array.isEmpty();
    }

    @Override
    public void push(Object o) {
        array.addLast((E) o);
    }


    @Override
    public E pop(){
        return array.removeLast();
    }
    @Override
    public E peek(){
        return array.getLast();
    }
    @Override
    public String toString (){
        StringBuilder res = new StringBuilder();
        res.append("Stack: ");
        res.append("【");
        for (int i = 0;i<array.getSize();i++){
            res.append(array.get(i));
            if (i!= array.getSize()-1){
                res.append(",");
            }
        }
        res.append("】 top");
        return res.toString();
    }
}

public interface Stack<E> {
    int getSize();
    boolean isEmpty();
    void push(E e);
    E pop();
    E peek();
}

public class Main {
    public static void main(String[] args) {
        ArrayStack<Integer> stack = new ArrayStack<>();
        for (int i = 0;i<5;i++){
            stack.push(i);
            System.out.println(stack);
        }
        stack.pop();
        System.out.println(stack);
    }

}

时间复杂度

三、栈的小练习

这里我们举例力扣（LeetCode）算法练习第20题——有效的括号

给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。

package stack;
import java.util.Stack;
public class Solution {
    public boolean isValid(String s){
        Stack<Character> stack = new Stack<Character>();
        for (int i=0;i<s.length();i++){
            char c = s.charAt(i);
            if (c == '(' || c== '['|| c== '{')
                stack.push(c);
            else {
                if (stack.isEmpty())
                    return false;

                char topChar = stack.pop();
                if (c==')' && topChar != '(')
                    return false;
                if (c==']' && topChar != '[')
                    return false;
                if (c=='}' && topChar != '{')
                    return false;
            }
        }
        return stack.isEmpty();
    }
}

可以看到，在力扣测试也是成功的

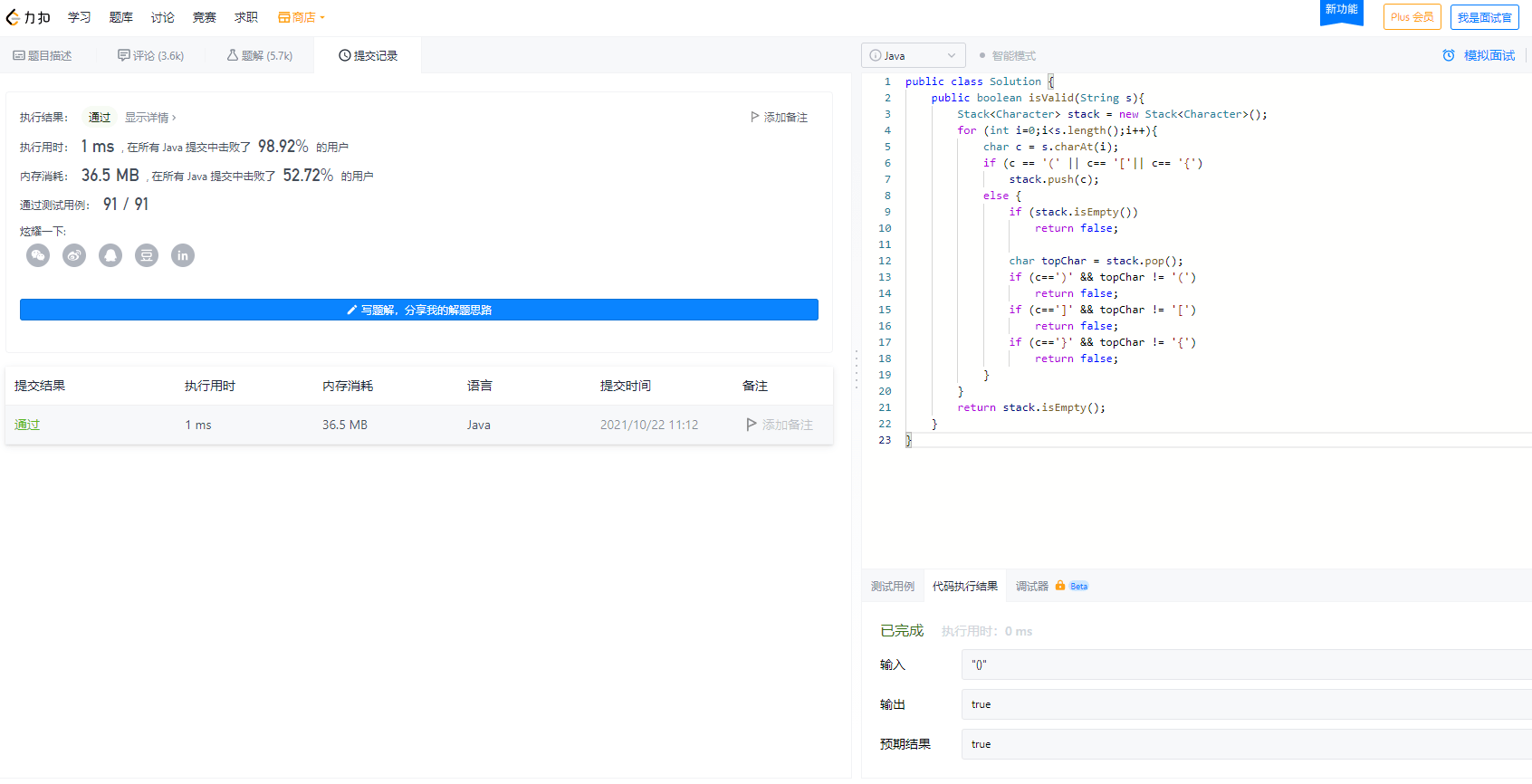
四、队列

什么是队列

队列的实现

代码小例子如下：

package Queue;

public class ArrayQueue<E> implements Queue {
    private Array<E> array;

    public ArrayQueue(int capacity) {
        array = new Array<E>(capacity);
    }

    public ArrayQueue() {
        array = new Array<E>();
    }

    @Override
    public int getSize() {
        return array.getSize();
    }

    @Override
    public boolean isEmpty() {
        return array.isEmpty();
    }

    @Override
    public void enqueue(Object e) {
        array.addLast((E) e);
    }

    public int getCapacity() {
        return array.getCapacity();
    }


    @Override
    public E dequeue() {
        return array.removeFirst();
    }

    @Override
    public Object getFront() {
        return array.getFast();
    }

    @Override
    public String toString() {
        StringBuilder res = new StringBuilder();
        res.append("Queue: ");
        res.append("front [");
        for (int i = 0; i < array.getSize(); i++) {
            res.append(array.get(i));
            if (i != array.getSize() - 1)
                res.append(", ");
        }
        res.append("] tail");
        return res.toString();
    }

    public static void main(String[] args) {
        ArrayQueue<Integer> queue = new ArrayQueue<Integer>();
        for (int i=0;i<10;i++){
            queue.enqueue(i);
            System.out.println(queue);
            if (i%3==2)
                queue.dequeue();
                System.out.println(queue);
        }
    }
}

public interface Queue<E> {
    int getSize();
    boolean isEmpty();
    void enqueue(E e);
    E dequeue();
    E getFront();
}

数组队列复杂度分析